Перевод числа из одной системы счисления в другую

1. Перевод целого числа десятичного кода в любую другую систему счисления осуществляется по следующему правилу: нужно делить исходное десятичное число на величину основания той системы счисления, в которую переводится число, а затем частное от деления снова делить на то же основание и так до тех пор, пока частное не окажется меньше делителя. Полученные остатки от деления и последнее частное будут представлять собой разряды числа в новой системе счисления. Чтение нового кода осуществляется с конца, т.е. последнее частное дает цифру старшего разряда.

Примеры:

1) перевести десятичное число 11 в двоичную систему счисления:

-
		-
				-
Направление чтения

Искомое двоичное число 1011, т.е. .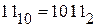

2) перевести десятичное число 61819 в шестнадцатеричную систему:

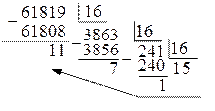
Поскольку 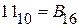, а 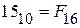, искомое шестнадцатеричное число запишется в виде 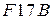, т.е. .

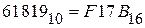2. Для перевода чисел из любой системы счисления в десятичную можно использовать запись этого числа в виде полинома (2.1). Выполнив сложение, получаем искомое десятичное число.

Пример.

Перевести восьмеричное число 745 в десятичную систему счисления:

.

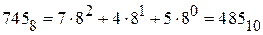Перевод в десятичный код может быть выполнен также по схеме Горнера. Процедура перевода следующая. Старший разряд исходного кода нужно умножить на основание переводимой системы счисления и полученное произведение сложить со следующим символом кода. Полученную сумму вновь умножить на основание и результат сложить со следующим символом и так продолжать до последнего (младшего) разряда кода. Для числа 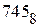указанные вычисления будут следующими:

.

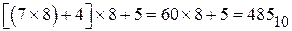Схема Горнера особенно удобна при переводе чисел из двоичной системы. Имеем: 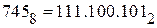. Переведем полученное двоичное число в десятичное:

Искомое десятичное число 485, т.е. .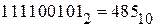

3. Перевод чисел из любой недесятичной системы счисления в другую недесятичную систему выполняется в следующей последовательности:

– по методике, изложенной в п. 2, перевести исходный код в десятичный;

– по методике, изложенной в п. 1, перевести полученный десятичный код во вторую систему счисления.

Решение упрощается, если основания подлежащих переводу систем удовлетворяют условию (2.3), т.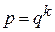е. , где 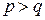, 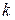– целое положительное число. При этом, если исходное число представлено в системе счисления с основанием 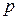, для получения его изображения в системе с основанием достаточно каждый символ исходного кода представить 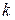-значным числом в системе счисления с основанием . Примеры такого перевода приведены в п. 2.1.2 для чисел 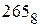и 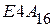. Если же исходное число представлено в системе счисления с основанием , для получения его изображения в системе с основанием 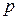нужно в последовательности символов исходного кода, начиная с младших разрядов, выделять группы по 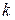знаков и каждой из этих групп поставить в соответствие число в системе счисления с основанием 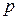. Если последняя группа окажется неполной, ее нужно дополнить нулями со стороны старших разрядов.

Примеры:

1) перевести двоичное число 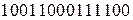в восьмеричную систему счисления ( ):

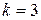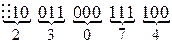
Получаем: ;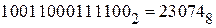

2) перевести то же двоичное число в шестнадцатеричную систему счисления ( ):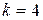

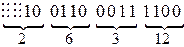
Получаем: .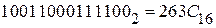

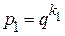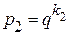Последние примеры показывают, что если , а , перевод чисел из системы счисления с основанием 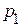в систему с основанием 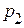и наоборот может выполняться через промежуточную систему счисления с основанием . В частности, так можно осуществлять перевод чисел из восьмеричной системы в шестнадцатеричную и наоборот через двоичный код, т.е. сначала исходное число представляется в двоичном коде, затем полученная двоичная комбинация разбивается на группы, каждой из которых ставится число во второй системе счисления.

Код Грея

Код Грея не базируется на системах счисления и применяется в технике аналого-кодового преобразования, где он позволяет свести к единице младшего разряда погрешность неоднозначности при считывании. Достигается это за счет того, что смежные числа этого кода отличаются только в одном разряде. Комбинации кода Грея, соответствующие десятичным числам от 0 до 15, приведены в таблице 2.1.

Таблица 2.1

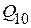
	Код Грея		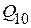Код Грея		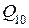Код Грея

Формируются комбинации кода Грея из обычного двоичного кода путем суммирования по модулю 2 исходной кодовой комбинации с такой же комбинацией, сдвинутой вправо на 1 разряд. Младший разряд в сдвинутой комбинации при этом отбрасывается.

Пример:

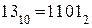
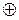
						– код Грея

Перевод числа из кода Грея в обычный двоичный осуществляется по следующему правилу: все предшествующие нули и первая единица со стороны старших разрядов остаются без изменения; последующие символы (0 и 1) остаются без изменения, если число единиц, им предшествующих в коде Грея, четно, и инвертируются, если число единиц нечетно.

Пример:

								– код Грея
								– двоичный код

Проверка:

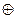
									– код Грея

<3456789>

---

Дата добавления: 2019-02-08; просмотров: 758;

---