Примеры построения эпюры продольных сил

Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а).

Делим брус на участки нагружения.

Участком нагружения считают часть бруса между внешними силами.

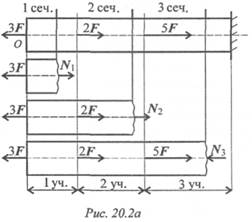На представленном рисунке 3 участка нагружения. Воспользуемся методом сечений и определим вну­тренние силовые факторы внутри каждого участка.

Расчет начинаем со свободного конца бруса, что­бы не определять величины реакций в опорах.

Участок 1: ∑F_z = 0; -3F + N1 = 0; N1 = 3F. Продольная сила положи­тельна, участок 1 растянут.

Участок 2: ∑F_z = 0; -3F + 2F + N₂ = 0; N₂ = F. Продольная сила по­ложительна, участок 2 растянут.

Участок 3: ∑F_z = 0; -3F + 2F + 5F - N₃ = 0; N₃ = 4F. Про­дольная сила отрицательна, участок 3 сжат. Полученное значение N₃ равно реакции в заделке.

Под схемой бруса строим эпюру продольной силы (рис. 20.26).

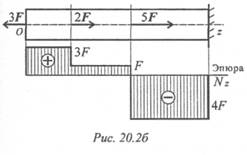Эпюрой продольной си­лы называется график рас­пределения продольной си­лы вдоль оси бруса.

Ось эпюры параллель­на продольной оси.

Нулевая линия прово­дится тонкой линией. Зна­чения сил откладывают от оси, положительные — вверх, отрицательные — вниз. В пределах одного участка значение силы не меняется, поэто­му эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

Правило контроля: в месте приложения внешней силы на эпюре должен быть скачок на величину приложенной силы.

На эпюре проставляются значения N_z. Величины продольных сил откладывают в заранее выбранном масштабе.

Эпюра по контуру обводится толстой линией и заштриховыва­ется поперек оси.

Изучая деформации при растяжении и сжатии, обнаруживаем, что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.

Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.

Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечению равномерно.

Принцип смягчения граничных условий гласит: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.