Линии влияния опорных реакций

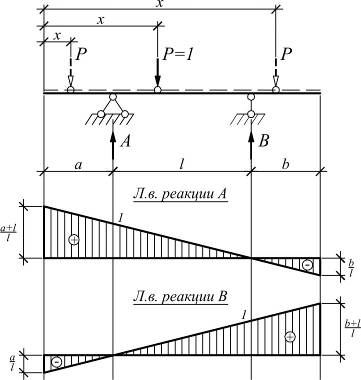
Рассмотрим, как изменяются величины опорных реакций при движении единичного груза по балке. Расположим груз P = 1 на расстоянии x от левого края балки.

Для определения реакции A составим уравнение суммы моментов всех сил относительно правой опоры B:

; ;

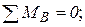
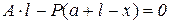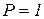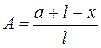– функция линейная

1. При ,	;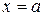
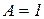2. При ,	;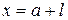

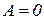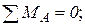
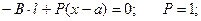
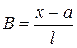функция линейная

1. При ,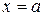
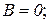
2. При ,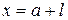

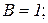
Л. в. опорной реакции называет график, показывающий изменение величины данной реакции при движении единичного груза по балке.

Порядок построения л. в. опорных реакций:

1. Под опорой, для реакции которой строим л. в., откладываем в выбранном масштабе отрезок равный +1;

2. Соединяем полученную точку с нулем под другой опорой;

3. Если имеются консоли, то линию влияния продляем на консольные участки.

Замечание: ординаты л. в. R – безразмерные величины.

Линии влияния M и Q для сечений расположенных в пролете балки

Линией влияния изгибающего момента называется графикпоказывающий изменение величины М в данном сечении при движении единичного груза по балке (см. рис. а).

Для построения л. в. рассмотрим 2 случая:

1.P = 1 левее сечения I

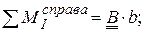b = const

Для построения левой прямой л. в. М_I необходимо взять л.в. реакции В и все ординаты умножить на b = const.

2.Р = 1 правее сечения I

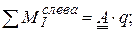a = const

Т.е чтобы построить правую прямую л. в. М_I необходимо все ординаты л.в. А умножить на а = const

Порядок построения л. в. М:

1. Под левой опорой откладываем со знаком (+) отрезок равный расстоянию от левой опоры до сечения;

2. Полученную точку соединяем с нулем под правой опорой;

3. Сносим по вертикале сечение на построенную правую прямую;

4. Точку пересечения вертикали справой прямой, соединяем с нулем под левой опорой (получаем левую прямую);

5. Если балка имеет консоли, то левую и правую прямые продляем на консольные участки;

6. Действительная часть левой прямой – левее сечения, правой – правее сечения.

Замечания:

1. Ордината y_K – представляет собой величину изгибающего момента в сечении 1, когда груз Р = 1 находится в точке К;

2. Ординаты л. в. М имеют размерность в линейных единицах (М).

Л. в. поперечной силы называется график, показывающий изменение величины Q при движении груза Р = 1 по балке (см. рис. б)

1) Р = 1 левее сечения I, рассматриваем правую часть балки

Q_I = –B;

2) Р = 1 правее сечения I, рассматриваем левую часть балки

Q_I = A;

Порядок построения л.в. Q:

1. Под левой опорой откладываем отрезок =+1 и соединяем полученную точку с нулем под правой опорой (получили правую прямую);

2. Под правой опорой откладываем отрезок = –1 и соединяем с нулем под левой опорой (левая прямая);

3. Если есть консоли, то левую и правую прямые продолжаем на консольные участки;

4. На полученные левую и правую прямые сносим сечения, действительная часть левой прямой – левее сечения, правой – правее сечения .

Замечание: ординаты л. в. Q – безразмерные величины.

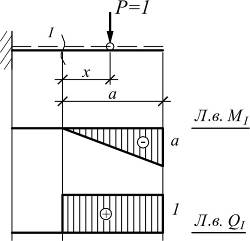
Построение л.в. М и Q для сечений расположенных на консольных участках балок

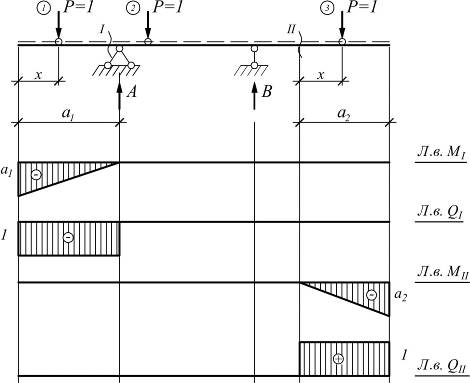
Сечение I-I

P = 1 левее сечения I.

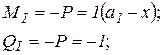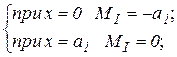
P = 1 правее сечения I MI = 0; QI = 0;

Сечение II-II

P = 1 левее сечения II MII = 0; QII = 0;

P = 1 правее сечения II

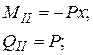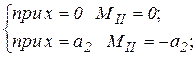
Порядок построения л.в. М:

1) под краем консоли откладываем со знаком (–) отрезок равный расстоянию от края консоли до сечения;

2) соединяем полученную точку с нулём под сечением.

Порядок построения л.в. Q:

1) под краем консоли откладываем отрезок равный +1 для правой консоли и -1 для левой консоли;

2) из полученной точки проводим прямую параллельную оси балки до сечения.

Замечание: аналогично строится л.в. М и Q для консольных балок.

Отличие между эпюрами М, Q и л.в. этих же величин.

Эпюры М и Q строятся от неподвижной нагрузки, приложенной к данной балки. По эпюрам мы можем определить значение М и Q в любом сечении балки.

Л. в. М и Q строятся для одного заданного сечения, при движении ед. груза по сооружению. Таким образом, по л. в. М и Q можно определить значение этих величин в одном зафиксированном сечении при различных положениях подвижной нагрузки.