Способ вырезания узлов

При определении усилий в стержнях ферм способом вырезания узлов, приходится иметь дело с плоской системой сходящихся сил.

Сущность способа состоит в следующем: поскольку вся ферма находится в равновесии, то и любой ее узел должен находиться в равновесии.

Т. к. для плоской системы сходящихся сил можно составить только два независимых уравнения ∑F_x = 0 и ∑F_y = 0, то расчет фермы следует начинать с двухстержневого узла и далее вырезать узлы, в которых сходится не более 2-х стержней с неизвестными усилиями.

Способ вырезания узлов применяется для наиболее простых ферм. Усилия в стержнях приходится определять через ранее найденные усилия, а это проводит к накоплению и увеличению ошибок в расчетах.

Рассмотрим пример расчета фермы методом вырезания узлов:

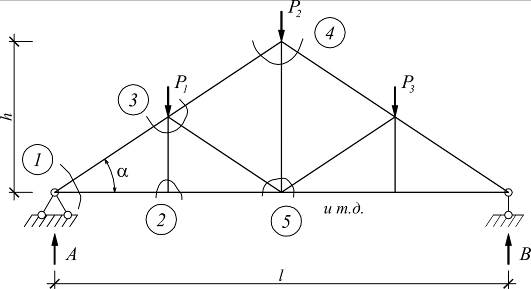
1)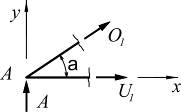

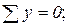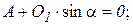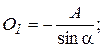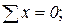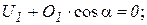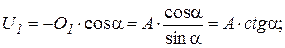
2)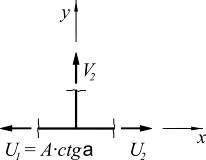

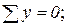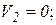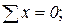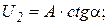
Частные случаи способа вырезания узлов:

1. Если в узле сходится два стержня и больше никаких сил к этому узлу не приложено, то усилия в обоих стержнях = 0.

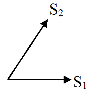
∑Y = 0; => S2 = 0; ∑X = 0 => S1 = 0;

2. Если к двухстержневому узлу приложена сила, направленная вдоль одного из них, то усилие в этом стержне равно силе по величине, но противоположно направлению, а во втором стержне усилия=0.

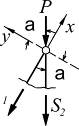
∑Y = 0 => S1 = -p; ∑X = 0 => S2 = 0;

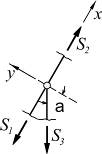
∑X = 0; => S1 = S2; ∑Y = 0 => S3 = 0;

3. Если в узле сходятся три стержня, из которых два направлены вдоль одной прямой, то усилия в третьем стержне равно нулю, а в первых двух равны между собой.

4. Если в узле сходятся три стержня, из которых два направлены вдоль одной прямой и есть нагрузка, направленная по оси третьего стержня, то усилия в этом стержне равно силе по величине, но противоположно направлено, а усилия в двух первых стержнях равны между собой.

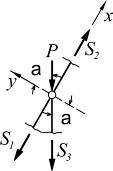
∑X = 0; => S1 = S2; ∑Y = 0 => S3 = -p;

5. В четырехстержневом узле, где стержни попарно направлены вдоль одной прямой, усилия также которого равны между собой.

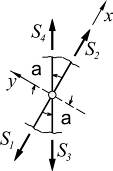
∑X = 0 => S3 = S4. ∑Y = 0; => S1 = S2;