Застосування регресійного аналізу: проблема прогнозу

На основі вибіркових даних табл. 3.2 нами було отримане таке рівняння вибіркової регресії:

,

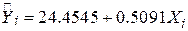(3.9.1)

де 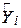– оцінювач істинного 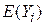, відповідного даному Х. Яка користь може бути отримана з цієї історичної регресії (historical regression)? Рівняння можна застосовувати для прогнозу або передбачення майбутніх споживацьких витрат Y, відповідних деякому даному рівню доходу Х. Можливі такі два види прогнозу:

1. Прогноз умовної середньої величини Y, відповідний вибраному Х, скажімо Х₀, тобто точки на самій лінії регресії популяції.

2. Прогноз індивідуальної величини Y, відповідної Х₀.

Ми називатимемо ці два прогнози середнім прогнозом й індивідуальним прогнозом.

Середній прогноз

Для більшої чіткості припустимо, що Х₀=100 і ми хочемо спрогнозувати E(Y/X₀=100). Зрозуміло, що рівняння історичної регресії (2.6.2) дає оцінку середнього прогнозу таким чином:

,

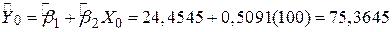(3.9.2)

де 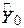– оцінка E(Y/X₀). Можна показати, що цей точковий прогноз - краща лінійна незміщена оцінка (best linear unbiased estimator, BLUE).

Оскільки 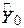є оцінкою, напевно числове її значення відрізняється від істинного. Різниця між двома цими величинами дасть деяке уявлення про помилку прогнозу. Для отримання цієї помилки нам необхідно знайти розподіл вибірки 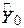. 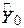, з формули (3.6.1), - нормально розподілена величина із середнім (b₁₊b₂Х₀) і її дисперсія задається такою формулою:

.

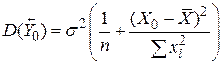(3.9.3)

Позначимо невідому 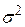її незміщеною оцінкою 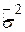. Тоді змінна

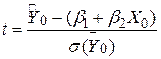
(3.9.4)

розподілена за законом розподілу Ст’юдента з N–2 степенями вільності. Отже, цей закон розподілу можна застосовувати для побудови довірчих інтервалів істинного E(Y₀|X₀) і перевірки гіпотез звичайним способом:

,

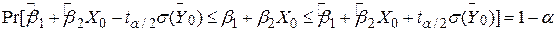(3.9.5)

де 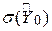отримано з (3.6.2):

.

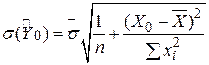Для наших даних одержуємо

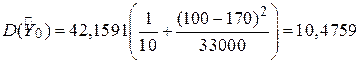і .

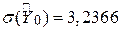Отже, 95%-й довірчий інтервал для істинного E(Y₀|X₀)=b₁₊b₂Х₀ задається формулою

.

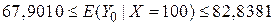(3.9.6)

Таким чином, для Х₀=100 у вибірках, що повторюються, 95 зі 100 інтервалів, подібних (3.6.5), міститимуть істинну середню величину; найкращим точковим оцінювачем буде 75,3645.

Якщо ми отримаємо 95%-ві довірчі інтервали, подібні (3.9.7), для кожного значення Х, наведених у табл. 1.3, ми отримаємо довірчу область (confidence band) для функції регресії популяції, показаної на рис. 3.6.

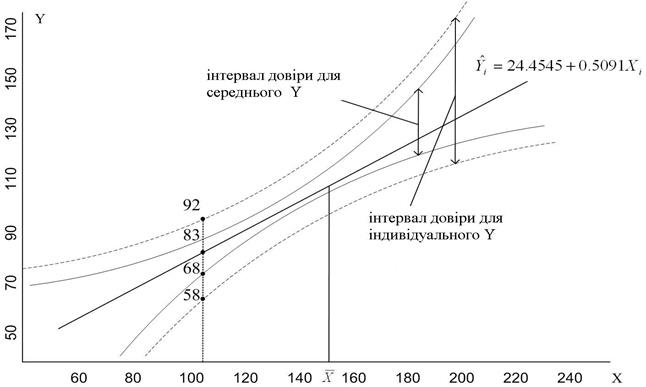
Рис. 3.6. Довірчі інтервали (області) для середньої Y й індивідуальної величини Y