Уравнение движения точки

Уравнение, определяющее положение движущейся точки в зави­симости от времени, называется уравнением движения.

Положение точки в каждый момент времени можно опреде­лить по расстоянию, пройденно­му вдоль траектории от некоторой неподвижной точки, рассматриваемой как начало отсчета (рис. 9.1). Такой способ задания дви­жения называется естественным.

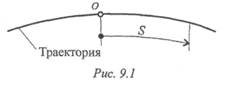
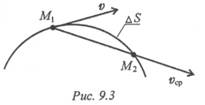
Таким образом, уравнение движения можно представить в виде S = f(t). Положение точки можно также определить, если известны ее координаты в зависимости от времени (рис. 9.2). Тогда в случае движения на плоскости должны быть заданы два уравнения: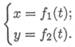

В случае пространственного движе­ния добавляется и третья координата z= f3(t).

Такой способ задания движения на­зывают координатным.

Скорость движения

Векторная величина, характеризующая в данный момент бы­строту и направление движения по траектории, называется скоро­стью.

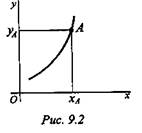
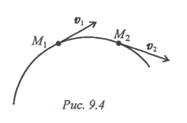
Скорость — вектор, в любой момент направленный по каса­тельной к траектории в сторону направления движения (рис. 9.3).

Если точка за равные промежутки времени проходит равные расстояния, то движение называ­ют равномерным. Средняя скорость на пути AS определяется как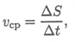

где AS — пройденный путь за время Д*; At — промежуток времени.

Если точка за равные промежутки времени проходит неравные пути, то движение называют неравномерным.

В этом случае скорость — величина переменная и зависит от времени v = f(t).

При рассмотрении малых промежутков времени (∆t —► 0) сред­няя скорость становится равной истинной скорости движения в дан­ный момент. Поэтому скорость в данный момент определяют как

производную пути по времени:

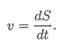
За единицу скорости принимают 1 м/с. Иногда скорость измеряют в км/ч,

1000
1 км/ч = ------ = 0,278 м/с.

Ускорение точки

Векторная величина, характеризующая быстроту изменения скорости по величине и направлению, называется ускорением точки.

Скорость точки при перемещении из точки М1 в точку M2 ме­няется по величине и направлению. Среднее значение ускорения за этот промежуток

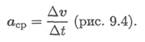
При рассмотрении бесконечно ма­лого промежутка времени среднее ускорение превратится в ускорение в данный момент:

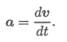
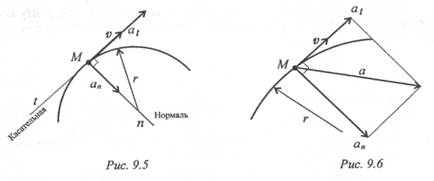
Обычно для удобства рассматривают две взаимно перпен­дикулярные составляющие ускорения: нормальное и касательное (рис. 9.5).

Нормальное ускорение а_п характеризует изменение скорости по направлению и определяется как

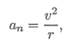
где г — радиус кривизны траектории в данный момент времени.

Нормальное ускорение всегда направлено перпендикулярно ско­рости к центру дуги.

Касательное ускорение аtхарактеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости, а

при замедлении оно направлено противоположно направлению век­тора скорости.

Формула для определения касательного ускорения имеет вид:

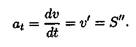
Значение полного ускорения определяется как
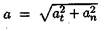(рис. 9.6).