Плоскопараллельное движение твердого тела
Плоскопараллельным, или плоским, называется такое движение твердого тела, при котором все точки тела перемещаются параллельно некоторой неподвижной в рассматриваемой системе отсчета плоскости.
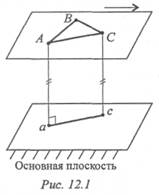
Плоскопараллельное движение можно изучать, рассматривая любое плоское сечение тела, параллельное неподвижной плоскости, называемой основной (рис. 12.1).
Все точки тела, расположенные на прямой, перпендикулярной к основной плоскости, движутся одинаково.
Плоскопараллельное движение изучается двумя методами: методом разложения сложного движения на поступательное и вращательное и методом мгновенных центров скоростей.
Метод разложения сложного движения на поступательное и вращательное
Плоскопараллельное движение раскладывают на два движения: поступательное вместе с некоторым полюсом и вращательное относительно этого полюса.
Разложение используют для определения скорости любой точки тела, применяя теорему о сложении скоростей (рис. 12.2).
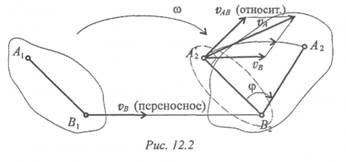
Точка А движется вместе с точкой В , а затем поворачивается
вокруг В с угловой скоростью ш, тогда абсолютная скорость точки А будет равна
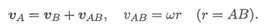
Примером плоскопараллельного движения может быть движение колеса на прямолинейном участке дороги (рис. 12.3).
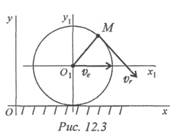
Скорость точки М vМ = ve + vr,
ve — скорость центра колеса переносная;
vr — скорость вокруг центра относительная.
уОх — неподвижная система координат,
у101Х1 — подвижная система координат, связанная с осью колеса.
Метод определения мгновенного центра скоростей
Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложное движение представляют в виде цепи вращений вокруг разных центров.
Задача сводится к определению положения мгновенного центра вращений (скоростей) (рис. 12.4).
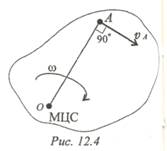
Мгновенным центром скоростей (МЦС) является точка на плоскости, абсолютная скорость которой в данный момент равна нулю.
Вокруг этой точки тело совершает поворот со скоростью ω.
Скорость точки А в данный момент равна va = ωOA,
т.к. va — линейная скорость точки А, вращающейся вокруг МЦС.
Существуют три способа определения положения мгновенного центра скоростей.
Первый способ. Известна скорость одной точки тела va и угловая скорость вращения тела ω(рис. 12.5).
Точку О находим на перпендикуляре к вектору скорости va.
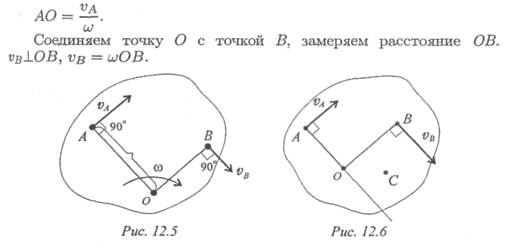
Второй способ. Известны скорости двух точек тела va и vB они не параллельны (рис. 12.6).
Проводим из точек А и В два перпендикуляра к известным векторам скоростей.
На пересечении перпендикуляров находим МЦС. Далее можно найти скорость любой точки 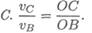
Третий способ. Известны скорости двух точек тела, и они параллельны (va║vB) (рис. 12.7).
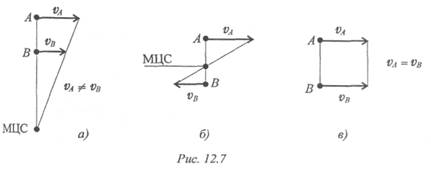
Соединяем концы векторов, МЦС находится на пересечении линии, соединяющей концы векторов с линией АВ ( рис. 12.7 ). При поступательном движении тела (рис. 12.7в) МЦС отсутствует.
Основные понятия и аксиомы динамики. Понятие о трении
Иметь представление о массе тела и ускорении свободного падения, о связи между силовыми и кинематическими параметрами движения, о двух основных задачах динамики.
Знать аксиомы динамики и математическое выражение основного закона динамики.
Знать зависимости для определения силы трения.
Содержание и задачи динамики
Динамика — раздел теоретической механики, в котором устанавливается связь между движением тел и действующими на них силами.
В динамике решают два типа задач:
— определяют параметры движения по заданным силам;
— определяют силы, действующие на тело, по заданным кинематическим параметрам движения.
При поступательном движении все точки тела движутся одинаково, поэтому тело можно принять за материальную точку.
Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка совпадает с центром тяжести тела.
При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
Поэтому динамику делят на динамику точки и динамику материальной системы.
Аксиомы динамики
Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и четвертый законы были известны Галилею. Механику, основанную на этих законах, называют классической механикой.
Первая аксиома (принцип инерции)
Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
Это состояние называют состоянием инерции. Вывести точку из этого состояния, т.е. сообщить ей некоторое ускорение, может внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела.
Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы — килограмм (кг).
Вторая аксиома (второй закон Ньютона — основной закон динамики)
Зависимость между силой, действующей на материальную точку, и сообщаемым ею ускорением следующая:
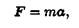
где т — масса точки, кг; а — ускорение точки, м/с2.
Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
Основной закон динамики в дифференциальной форме:

На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли:
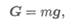
где g = 9,81 м/с , ускорение свободного падения.
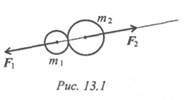
Третья аксиома (третий закон Ньютона) Силы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны (рис. 13.1):
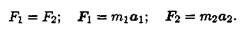
Откуда 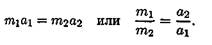
При взаимодействии ускорения обратно пропорциональны массам.
Четвертая аксиома(закон независимости действия сил)
Каждая сила системы сил действует так, как она действовала бы одна.
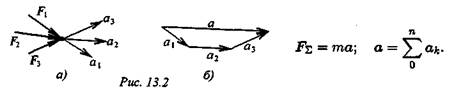
Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности (рис. 13.2):
Дата добавления: 2019-02-08; просмотров: 1389;











