Условие равновесия произвольной плоской системы сил

1. При равновесии главный вектор системы равен нулю (Fгл = 0).

Аналитическое определение главного вектора приводит к выводу:

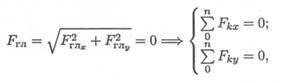
где Fkx и Fky — проекции векторов на оси координат.

2. Поскольку точка приведения выбрана произвольно, ясно, что
при равновесии сумма моментов сил системы относительно любой
точки на плоскости должна равняться нулю:

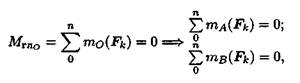
где А и В — разные точки приведения.

Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:

Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и до­статочно, чтобы алгебраическая сумма проекций всех сил систе­мы на любую ось равнялась нулю и алгебраическая сумма момен­тов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю.

Получим основную форму уравнения равновесия:

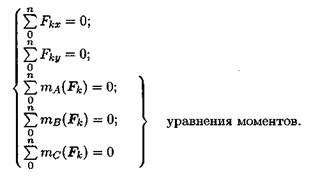
Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно соста­вить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.

Таким образом, имеем пять независимых уравнений равновесия.

Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.

Для разных случаев используются три группы уравнений рав­новесия.

Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:

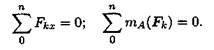
Ось Ох системы координат параллельна линии действия сил.