Просвечивающая электронная микроскопия
Метод электронномикроскопического просвечивания имеет много общего с рентгеновской топографией — в том и другом случае используются дифракционные эффекты от области с искаженной структурой, окружающей дефекты кристаллической решетки.
Просвечиванию подвергаются образцы в виде тонких фольг. Увеличение современных микроскопов таково, что в металлах удается разрешить отдельные атомные плоскости, находящиеся на расстояниях 2—3 А.
Для качественного описания контраста, возникающего под влиянием дислокаций в фольге, рассмотрим модель фольги. Предположим, что образец содержит на участке Е краевую дислокацию, параллельную поверхности фольги. Предполагаем, что фольга ориентирована таким образом, что почти удовлетворяется брэгговское условие для дифракции от этой системы плоскостей. На фольгу падает параллельный пучок электронов, который частично проходит через фольгу, а частично дифрагирует.
Рассмотрим область, лежащую непосредственно вблизи дислокации, в которой часть атомных плоскостей деформирована. Так как плоскость фольги такова, что почти удовлетворяется условие дифракции, то можно считать, что с одной стороны от дислокации вследствие искажений решетки это условие будет удовлетворяться полностью, тогда, конечно, с другой стороны от дислокации отклонение будет больше среднего.
В результате окажется, что интенсивность дифрагированного луча больше средней Величин в некоторой точке Е1 и меньше — в точке Е2. В электронном микроскопе при обычных условиях эксперимента диафрагма ограничивает электронный пучок и на флюоресцирующий экран попадают только прошедшие лучи. Следовательно, изображение точки E1 будет менее интенсивном, а точки Е2 более интенсивным, т. е. на микрофотографии возникает черная линия.
Такое же рассуждение можно провести для винтовой дислокации, для которой вектор Бюргерса и линия дислокации совпадают по направлению. Рассмотрим систему плоскостей, перпендикулярных к вектору Бюргерса. Сечения, проведенные по обе стороны от линии дислокации, показывают, что рассматриваемые плоскости в этих сечениях наклонены в разные стороны.
Следовательно, как и в случае краевой дислокации, интенсивность прошедшего пучка электронов по одну сторону от дислокации будет больше, а по другую меньше, чем для совершенного материала. Винтовая дислокация также будет изображаться на электронномикроскопическом снимке в виде черной линии, несколько смещенной по сравнению с действительным расположением дислокации в фольге.
Определение знака вектора Бюргерса основано на следующих соображениях. Из сказанного выше следует, что эффекты дислокационного контраста могут наблюдаться только для тех плоскостей решетки, которые искажаются под действием дислокаций. Предположим, что атомные плоскости, расположенные параллельно вектору Бюргерса, не деформируются, так как все смещения в решетке параллельны этим плоскостям. Следовательно, отражения от таких плоскостей не дадут дислокационного контраста. Итак, для плоскостей, дифракционный вектор которых удовлетворяет условию g х b = 0, не наблюдается дифракционного контраста.
Для определения знака вектора Бюргерса, таким образом, достаточно найти две системы плоскостей с дифракционными векторами g1 и g2, удовлетворяющих условиям погашения (т. е. g1 x b = 0 И g2 x b = 0), и тогда направление вектора Бюргерса будет совпадать с направлением (g1 x g2).
Для дислокаций, которые .перпендикулярны к поверхности фольги, в случае контраста от вертикальных плоскостей (100) в зоне сжатия d<d100 а в зоне расширения d>d100. Предположим, что брэгговские условия почти удовлетворяются для плоскостей (100), причем угол падения несколько меньше брэгговского. Тогда условия дифракции будут лучше удовлетворяться в растянутой области и хуже — в сжатой, первая будет на микрофотографии темнее, а вторая светлее, чем фон. Для отражения от плоскостей (010) не будет наблюдаться контраста, так как для них g x b = 0.
Очевидно, при изменении знака дислокации белые и черные участки будут меняться местами. Для винтовой дислокации, перпендикулярной к плоскости фольги, модель дифракционного контраста более сложна и связана со скручиванием атомных плоскостей, при этом меняются местами темные и светлые участки при переходе от левого к правому вращению.
Количественные расчеты интенсивности базируются на соотношениях, связывающих амплитуду дифрагированной волны электронов с характеристиками кристаллической решетки исследуемого металла и геометрической схемой съемки.
Принцип расчета при применении кинематической теории рассеяния электронов заключается в следующем. Предполагается, что фазовый контраст может привести к различию в интенсивности электронов, дифрагированных в областях, окружающих дефекты. Исходя из величин смещений атомов вокруг дислокаций, можно определить амплитуду и фазу электрических векторов дифрагированных лучей.
Интенсивность дифрагированных лучей пропорциональна квадрату амплитуды волны, возникающей в результате суммирования амплитуд в столбике, мысленно вырезанном в кристаллах и параллельном дифрагированной волне. В совершенном кристалле результирующая сумма равна

где rj — вектор решетки, определяющий положения атомов в элементарной ячейке, s — мера векторного отклонения от узла обратной решетки, F — структурный множитель, величина которого связана с расположением атомов в элементарной ячейке.
Понятие обратной решетки часто применяется при рентгеноструктурном, электронографическом, нейтронографическом и электронномикроскопическом методах анализа кристалла. Это понятие можно ввести следующим образом. Пусть в кристаллической решетке элементарная ячейка определяется некоторыми тремя осями а, b, с. Семейство плоскостей, параллельных векторам b и с, т. е. плоскости (100), изображаем вектором а*, перпендикулярным к этим плоскостям, причем за длину этого вектора принимаем величину, обратную соответствующему межплоскостному расстоянию. Вместе с несколькими дополнительными условиями это может быть записано следующим образом:
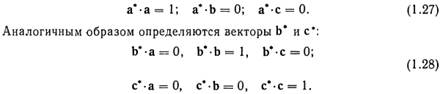
Точечная решетка, построенная на векторах а*, b*, с*, называется обратной решеткой для прямой решетки, построенной на векторах а, b, с.
Возвращаясь к уравнению (1.26), необходимо отметить, что сумма векторов амплитуды может быть выражена интегралом по столбику. Тогда интенсивность дифрагированного излучения для идеального кристалла будет равна
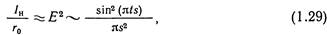
где t — толщина кристалла.
Если кристалл содержит дефект (дислокацию), вызывающий изменение векторов решетки rj на величину R, то выражение (1.26) переходит в
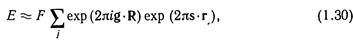
где g — вектор обратной решетки (дифракционный вектор) для брэгговского отражения.
Так же, как и выше, эта сумма может быть сведена к интегралу, например, по столбику, находящемуся на расстоянии х1 от винтовой дислокации AB. В результате расчета получают амплитуды и соответствующие интенсивности лучей в функции параметра β = 2πsx1. Форма контуров интенсивности зависит от порядка отражения. Эффективная полу ширина профиля интенсивности составляет
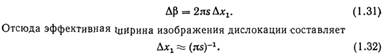
Следует специально ответить, что профиль интенсивности для дислокации обладает очень сильной асимметрией и контраст обычно почти полностью наблюдается Только с одной стороны от дислокации (центр дислокации совпадает с ß = 0).
Результаты вычислений, рассмотренных выше, качественно хорошо совпадают с данными экспериментальных исследований тонких металлических фольг. Более точное совпадение теории с экспериментом удается получить, используя динамическую теорию дифракции рентгеновских лучей, в которой в отличие от кинематической теории, изложенной выше, учитываются так>не эффекты взаимодействия падающих и рассеянных воли. В частности, было получено выражение для ширины изображения дислокации
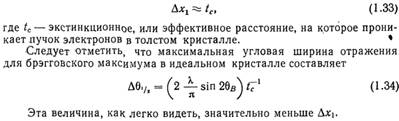
Дата добавления: 2023-03-16; просмотров: 753;











