ОСНОВИ ТЕРМОДИНАМІКИ НЕЗВОРОТНИХ ПРОЦЕСІВ
Дослідження біофізичних процесів, що відбуваються в реальних системах, методами рівноважної термодинаміки часто є неадекватним наближенням. У загальному випадку фізичні і біофізичні об'єкти не знаходяться в положенні рівноваги. В них з кінцевою швидкістю протікають незворотні процеси, які прагнуть повернути систему в стан рівноваги. Добре відомими прикладами можуть бути процеси теплопровідності з характерним часом встановлення рівноваги або, як його ще називають, часом релаксації 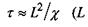 - лінійний розмір системи,
- лінійний розмір системи, 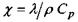 - коефіцієнт температуропровідності,
- коефіцієнт температуропровідності, 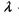 - коефіцієнт теплопровідності,
- коефіцієнт теплопровідності, 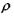 - густина,
- густина, 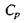 - ізобарна теплоємність); процеси дифузії з часом релаксації
- ізобарна теплоємність); процеси дифузії з часом релаксації 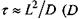 - коефіцієнт дифузії); процеси внутрішнього тертя з часом релаксації
- коефіцієнт дифузії); процеси внутрішнього тертя з часом релаксації 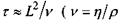 - кінематична в'язкість,
- кінематична в'язкість, 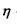 - динамічна в'язкість) та ін.
- динамічна в'язкість) та ін.
Термодинаміка незворотних процесів, що є феноменологічною основою для вивчення незворотних процесів у різних системах, в тому числі і біофізичних, спирається на такі положення та поняття: лінійний закон, принцип симетрії кінетичних коефіцієнтів, закони збереження, виробництво ентропії, спряження потоків, стаціонарний стан, теорема Пригожина та ін.
Лінійний закон
Лінійний закон становить узагальнення відомих емпіричних фактів, що формулюються у вигляді таких законів:
а) закони Фіка, що пов'язує потік частинок 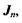 тобто кількість частинок, які за одиницю часу перетинають одиницю площі в перпендикулярному напрямку, і різницю (градієнт) концентрації
тобто кількість частинок, які за одиницю часу перетинають одиницю площі в перпендикулярному напрямку, і різницю (градієнт) концентрації 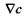 за допомогою співвідношення
за допомогою співвідношення
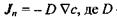 - коефіцієнт дифузії;
- коефіцієнт дифузії;
б) закон Фур'є, що пов'язує потік тепла 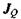 і різницю (градієнт) температури
і різницю (градієнт) температури 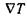 за допомогою співвідношення
за допомогою співвідношення 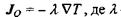 - коефіцієнт теплопровідності;
- коефіцієнт теплопровідності;
в) закон Ома, що пов'язує потік заряду (густину електричного струму) 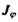 і градієнт потенціалу електричного поля
і градієнт потенціалу електричного поля 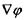 за допомогою співвідношення
за допомогою співвідношення 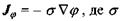 - коефіцієнт електропровідності.
- коефіцієнт електропровідності.
Нагадаємо, що градієнт 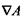 певної скалярної величини
певної скалярної величини 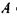 є вектор, який за модулем дорівнює максимальному значенню похідної
є вектор, який за модулем дорівнює максимальному значенню похідної 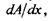 а за напрямком співпадає з напрямком зростання величини
а за напрямком співпадає з напрямком зростання величини 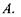
Процеси переносу, в яких градієнт даної властивості викликає потік цієї ж фізичної властивості, називаються прямими процесами переносу. Очевидно, що перераховані вище приклади відносяться саме до такого класу процесів переносу. Окрім прямих, існують непрямі (перехресні) процеси переносу, в яких градієнт однієї фізичної властивості викликає потік іншої фізичної властивості.
Розглянемо приклад так званих термодифузійних явищ. Нехай у деякому середовищі спостерігаються два градієнти: концентрації 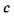 і температури
і температури 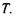 Тоді в такому середовищі виникають потоки частинок і тепла, причому
Тоді в такому середовищі виникають потоки частинок і тепла, причому
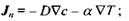
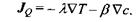
Процес виникнення потоку частинок під дією градієнта температури називається ефектом Соре (другий доданок у рівнянні для 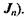 Зворотний процес, пов'язаний з виникненням потоку тепла під дією градієнта концентрації, називається ефектом Дюфура. Ще одним прикладом непрямого процесу переносу є термоелектропровідність - виникнення потоку електричного заряду під дією градієнта температури.
Зворотний процес, пов'язаний з виникненням потоку тепла під дією градієнта концентрації, називається ефектом Дюфура. Ще одним прикладом непрямого процесу переносу є термоелектропровідність - виникнення потоку електричного заряду під дією градієнта температури.
Для узагальнення наведених вище емпіричних законів розглянемо:
а) термодинамічні сили
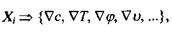
що пов'язані з градієнтами різних фізичних величин (концентрації, температури, потенціалу електричного поля, швидкості тощо);
б) потоки
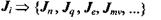
кількості частинок, тепла, електричного заряду, імпульсу тощо.
Лінійний закон термодинаміки незворотних процесів стверджує: кожний потік становить лінійну функцію від термодинамічних сил, тобто:
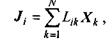 (5.7)
(5.7)
де 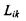 - так звані кінетичні коефіцієнти;
- так звані кінетичні коефіцієнти; 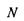 - загальна кількість термодинамічних сил в системі. Зауважимо, що лінійний закон справедливий при порівняно невеликих відхиленнях системи від положення рівноваги, коли градієнти фізичних властивостей (термодинамічні сили) є малими. При великих відхиленнях від положення рівноваги необхідно враховувати старші по
- загальна кількість термодинамічних сил в системі. Зауважимо, що лінійний закон справедливий при порівняно невеликих відхиленнях системи від положення рівноваги, коли градієнти фізичних властивостей (термодинамічні сили) є малими. При великих відхиленнях від положення рівноваги необхідно враховувати старші по 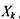 доданки - квадратичні, кубічні тощо. Природно, що така теорія ускладнюється. Тут розглядається лише лінійний варіант термодинамічної теорії незворотних процесів.
доданки - квадратичні, кубічні тощо. Природно, що така теорія ускладнюється. Тут розглядається лише лінійний варіант термодинамічної теорії незворотних процесів.
Відзначимо ще один, здавалося б очевидний факт, що носить назву принципу Кюрі: лінійний закон повинен зв'язувати потоки і термодинамічні сили однієї і тієї самої скалярної, векторної (в загальному випадку - тензорної) розмірності. Іншими словами, в кожне рівняння лінійного закону повинні входити або скалярні величини, такі як тиск (ці величини називаються ще тензорами нульового рангу) або векторні величини, такі як градієнти концентрації, температури, потенціалу електричного поля, а також потоки частинок, тепла, електричного заряду (ці величини називаються ще тензорами першого рангу) або так звані тензори другого рангу, якими є потік імпульсу та градієнт швидкості. Принцип Кюрі дає змогу встановити достатньо нетривіальні факти, згідно з якими, наприклад, потік частинок, що є векторною величиною, не може викликатися просторовими похідними від швидкості, тобто тензорними величинами 2-го рангу) та ін.
Дата добавления: 2020-11-18; просмотров: 713;











