Стаціонарний стан відкритих систем і теорема Пригожина щодо мінімуму виробництва ентропії

Розглянемо поняття стаціонарного стану, котре відіграє важливу роль в термодинамічному описанні відкритих систем.

Повна зміна ентропії 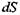у відкритій системі може бути представлена як сума двох доданків

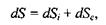(5.16)

що описують в загальному вигляді такі процеси:

1) процеси зміни ентропії всередині системи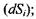

2) процеси зміни ентропії через взаємодію відкритої системи з навколишнім середовищем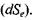

Коли б всередині досліджуваної системи відбувалися лише зворотні процеси, то зміна ентропії була б відсутня 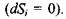Оскільки всередині реальної системи протікають незворотні дисипативні процеси, в результаті яких наробляється ентропія, то 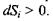Щодо знака величини 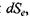то він може бути довільним і залежить від того, відбувається поступлення ентропії в систему або відтік ентропії з неї, пов'язаний з потоками частинок, тепла та іншими процесами переносу через поверхню, що обмежує виділений об'єм досліджуваної системи.

Стаціонарним називається такий стан системи, при якому ентропія всієї відкритої системи 5 зберігається, тобто повна зміна ентропії дорівнює нулю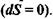

Із умови постійності ентропії 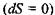і рівняння (5.16) безпосередньо випливає, що 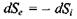. Тоді в силу позитивності зміни ентропії 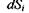за рахунок дисипативних процесів, що відбуваються всередині системи, зміна ентропії 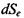через взаємодію відкритої системи з довкіллям повинна бути від'ємною 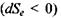і достеменно рівною за модулем зміні ентропії 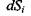всередині системи. Подібна реалізація умови стаціонарності відкритої системи стає можливою, якщо ентропія, що наробляється всередині системи, повністю переходить в навколишнє середовище. Іншими словами, можна стверджувати, що відкриті системи у стаціонарному стані живляться негентропією (від'ємною ентропією)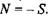

Пригожий довів, що у стаціонарному стані виробництво ентропії мінімальне 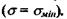Це твердження має назву "теорема Пригожина". Розглянемо міркування, що спонукають до встановлення цієї теореми.

Дійсно, з отриманих у параграфі 3.2.2 формул для виробництва ентропії 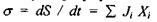та лінійного закону 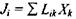маємо

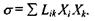(5.17)

Для спрощення обмежимося випадком двох термодинамічних сил і відповідно двох потоків. Тоді, беручи до уваги принцип симетрії кінетичних коефіцієнтів 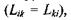можна записати такий вираз для виробництва ентропії:

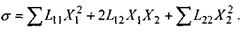
Обчислимо часткові похідні від виробництва ентропії а за термодинамічними силами 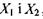, а саме:

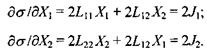
Отже, коли в стаціонарному стані відкритої системи потоки 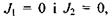то виробництво ентропії приймає екстремальне значення. В силу додатної визначеності квадратичної форми 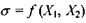і пов'язаної з цим позитивності других похідних

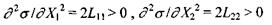
цей екстремум є мінімум (див. розділ 1 в першому томі), тобто виробництво ентропії у стаціонарному стані приймає мінімально можливе значення.

Принцип мінімуму виробництва ентропії у стаціонарному стані відкритої системи має надзвичайно важливе значення. Він дає кількісний критерій, що допомагає визначити напрямок розвитку (еволюції) відкритої системи будь-якої складності, а саме: якщо у відкритій системі відбуваються незворотні процеси поблизу термодинамічної рівноваги, то по зменшенню виробництва ентропії у такій системі можна передбачити її перехід у стаціонарний стан. Іншими словами, критерієм наближення системи до стаціонарного стану є від'ємність похідної від виробництва ентропії за часом, тобто виконання нерівності

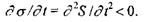(5.18)

Теорема Пригожина пояснює також принципову стійкість стаціонарних станів відкритих систем. Справді, якщо відкрита система самодовільно виходить з свого стаціонарного стану через флуктуації, то в ній відбувається збільшення швидкості виробництва ентропії 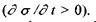Тоді через теорему Пригожина необхідним наслідком подібної зміни стану системи мають бути такі процеси всередині системи, при яких вона знову повернеться до свого початкового стаціонарного стану. Принцип мінімуму виробництва ентропії (теорема Пригожина) відіграє таку саму роль для відкритих систем, як принцип Ле Шательє-Брауна, що пояснює стійкість рівноважних систем: будь-який зовнішній вплив, який виводить систему з положення рівноваги, викликає в ній такі процеси, які прагнуть послабити результат цих зовнішніх впливів.

<69 70 717273 74 75 >

Дата добавления: 2020-11-18; просмотров: 401;