Рівняння електричних коливань

<18 19 202122 23 24 >

Розглянемо коло, до якого входить джерело струму з електрорушійною силою ε (в загальному випадку - змінною), індуктивність 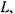ємність С та активний опір R, що з'єднані послідовно (мал. 2.25). Запишемо вираз, який пов'язує спад напруги на опорі напругу на конденсаторі 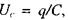напругу на індуктивності 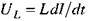та е.р.с. джерела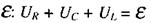

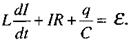
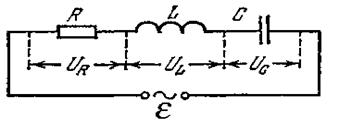
Мал. 2.25.

Оскільки за означенням 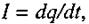після диференціювання за часом, одержимо диференційне рівняння електричних коливань:

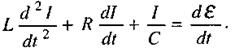(2.66)

Це рівняння виражає залежність сили струму від часу і є лінійним неоднорідним диференційним рівнянням другого порядку з постійними коефіцієнтами. Аналогічне рівняння можна отримати і для інших електричних величин (наприклад, заряду на конденсаторі q).

Вільні гармонічні коливання. Якщо джерело має постійну в часі ЕРС, тобто 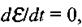то рівняння (2.66) стає однорідним. За аналогією з механічними коливаннями це є рівняння згасаючих коливань

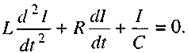(2.67)

За відсутності опору 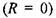рівняння (2.67) перетворюється в рівняння вільних гармонічних коливань

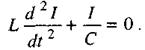
Розділивши ліву частину цього рівняння на 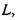матимемо:

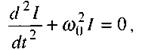(2.68)

де 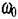- власна частота вільних електричних коливань

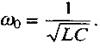(2.69)

Рівняння (2.68) має своїм розв'язком гармонічну функцію

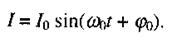(2.70)

Вираз, котрий стоїть під знаком синуса (або косинуса), називають фазою коливань 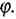У даному випадку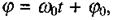де 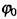- початкова фаза. Мінімальний проміжок часу, через який фаза повторює своє значення, називається періодом коливань. Період власних коливань

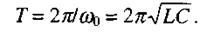(2.71)

Ця формула носить назву формули Томсона. Із зменшенням індуктивності котушкита ємності конденсатора С зменшується період коливань, а значить зростає їхня частота.

2.4.2. Вимушені електричні коливання, змінний струм

Розглянемо тепер електричні коливання, які виникають при наявності в колі генератора ЕРС, яка періодично змінюється.

Коло з активним (омічним) опором. Спочатку розглянемо частинний випадок, коли генератор змінного струму замкнений на зовнішнє коло, яке ,'містить лише активний опір(мал. 2.26). Припустимо, що в колі існує змінний струм:

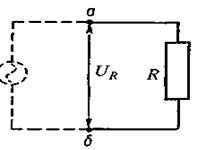
Мал. 2.26.

Застосовуючи закон Ома, визначимо, за яким законом змінюється напруга на активному опорі

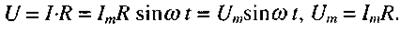(2.72)

Мал. 2.27. Мал. 2.28.

Ця рівність показує, що між коливаннями 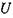та немає зсуву фаз: напруга і струм одночасно досягають максимальних значень і одночасно перетворюються в нуль (мал. 2.27). Наочно це можна зобразити за допомогою векторної діаграми. Величини, які змінюються за гармонічним законом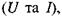будемо розглядати як вектори, модуль яких дорівнює їхньому амплітудному значенню, а кут між ними - різниці фаз. Вісь діаграми виберемо так, щоб вектор I збігівся з нею за напрямком. Цю вісь називають віссю струмів. Тоді вектор, що зображає коливання напруги, буде направлений вздовж осі струмів (мал. 2.28). Довжина цього вектора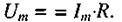

Коло з індуктивністю.Розглянемо випадок, коли ділянка кола містить лише індуктивність (мал. 2.29). Тоді за законом електромагнітної індукції Фарадея електрорушійна сила

(ЕРС) індукції 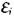визначається швидкістю зміни магнітного потоку 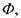тобто 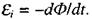У випадку самоіндукції магнітний потік Ф прямо пропорційний силі струму 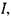що тече по контуру, тобто 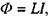де 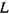- індуктивність контура.

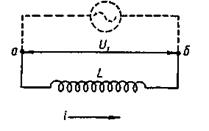
Мал. 2.29.

Таким чином, при наявності змінного струму в котушці індукується ЕРС самоіндукції, величина якої дорівнює 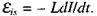Відповідно до закону Ома для повного кола сума всіх ЕРС за відсутності активного опору повинна дорівнювати нулю, тобто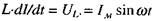

Якщо сила струму в колі змінюється за законом 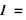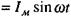, то для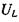отримуємо:

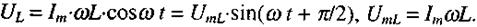(2.73)

Порівнюючи відношення для амплітудних значень І_т та U_m із законом Ома, бачимо, що роль опору відіграє величина 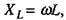яку називають індуктивним опором. Також видно, що сила струму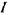та напруга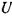зсунуті за фазою одна відносно іншої (мал. 2.30) на величину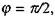причому напруга в будь-який момент часу випереджає силу струму. На векторній діаграмі це зобразиться так, як показано на мал. 2.31.

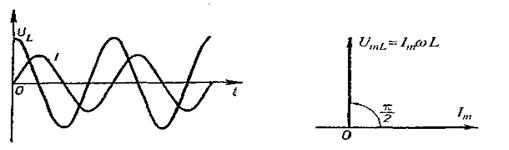
Мал. 2.30. Мал. 2.31.

Коло з ємністю. Розглянемо третій частинний випадок, коли ділянка кола містить лише конденсатор ємності С (мал. 2.32). Як і раніше, будемо вважати, що сила струму змінюється за законом 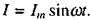Різниця потенціалів між пластинами конденсатора 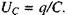Але ж сила струму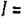 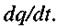Тоді

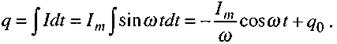(2.74)

Постійна інтегрування визначає заряд, який не пов'язаний з коливаннями струму, і тому можна покласти 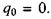Отже,

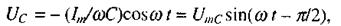(2.75)

де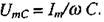

Порівнюючи (2.75) із законом Ома, бачимо, що роль опору відіграє величина 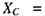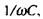яка називається ємнісним опором. Ємнісний опір зменшується із зростанням частоти. Бачимо також, що сила струму та напруга зсунуті по фазі на величи ну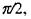причому сила струму в будь-який момент часу випереджає напругу (мал. 2.33).

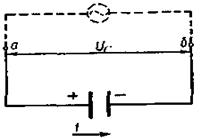
Мал. 2.32.

Отриманий результат зобразимо за допомогою векторної діаграми (мал. 2.34). Вектор, що відповідає коливанням напруги, повернений у від'ємному напрямі (за годинниковою стрілкою) на кут 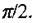Довжина вектора дорівнює амплітуді напруги .

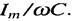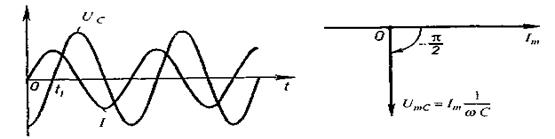
Мал. 2.33. Мал. 2.34.

2.4.3. Повний опір кола змінного струму (імпеданс). Закон Ома для кола змінного струму

Отримані результати дозволяють знайти співвідношення між коливаннями сили струму та напруги в будь-якому колі. Розглянемо спочатку коло, в яке послідовно ввімкнені активний опір R, ємність С та індуктивність L (мал. 2.35). Сила струму в загальному випадку відрізняється за фазою від напруги U і є однаковою для кожного елемента кола: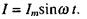

Оскільки при послідовному з'єднанні додаються напруги, то шукану напругу можна подати як суму спадів напруг на окремих ділянках: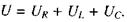Для додавання цих трьох гармонічних коливань скористаємося векторною діаграмою. Врахуємо, що напруга на омічному опорі синфаз-на з силою струму, напруга на індуктивності випереджає силу струму на 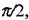а на ємності ж відстає на 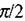(мал. 2.36). Додаючи два останні коливання 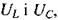ми отримаємо одне гармонічне коливання, яке зображується вектором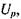перпендикулярним до осі струмів; довжина цього вектора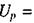 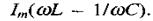Цей спад напруги називається реактивною складовою спаду напруги, а відповідний опір (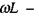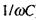) - реактивним опором. Таким чином, повний спад напруги 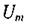можна розглядати як суму двох гармонічних коливань: активної складової 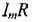та реактивно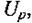ї які

відрізняються за фазою на 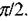Величину 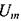можна знайти за теоремою Піфагора (мал. 2.36):

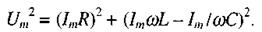(2.76)

і \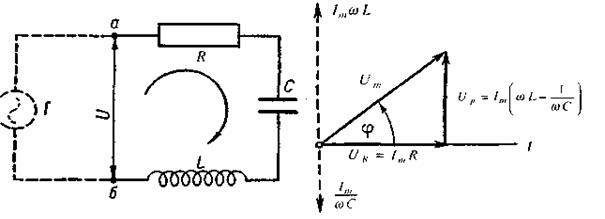

Мал. 2.35. Мал. 2.36.

Для макимального значення повного спаду напруги в контурі закон Ома має вигляд 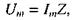де Z - повний опір кола змінного струму, або імпеданс. Порівнюючи два останніх рівняння, отримуємо вираз для імпедансу Z. При послідовному увімкненні в коло змінного струму активного опору, індуктивності і ємності повний опір кола (імпеданс) дорівнює:

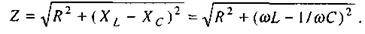(2.77)

Зсув фаз φ між силою струму і напругою визначається із трикутника напруг (мал. 2.36):

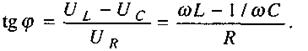(2.78)

Із (2.77) бачимо, що при 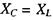реактивний опір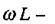 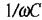дорівнює нулю, а імпенданс Z дорівнює активному опору 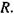У цьому випадку 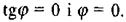Це означає, що сила струму 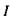і напруга 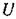змінюються в однакових фазах. Цей випадок має назву резонансу напруг. При резонансі напруг частота генератора збігається з власною частотою, тобто задовольняє формулу Томсона.

При паралельному з'єднанні ємності С, індуктивності L та активного опору R імпеданс Z можна знайти із співвідношення

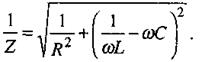(2.79)

У випадку рівності ємнісного та індуктивного опорів при паралельному сполученні спостерігається резонанс струмів. Опір кола при цьому буде максимальним, а сила струму мінімальною, хоча струми через конденсатор та котушку можуть бути достатньо великими, однак вони вза-ємоврівноважуються.

2.4.4. Імпеданс біологічних тканин

Як показує експеримент, для біологічних тканин характерні великі значення кута зсуву фаз між силою струму і напругою, причому сила струму випереджає за фазою напругу. Це свідчить, що частка ємнісного опору в біологічних об'єктах значна. Наведемо деякі значення кута зсуву фаз 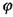при частоті 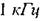для різних біооб'єктів:

Як правило, індуктивністю біологічних об'єктів нехтують (при частотах 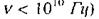і вважають, що їхній імпеданс дорівнює геометричній сумі активного R і ємнісного 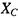опорів. Для характеристики пропускання струму живими клітинами використовують еквівалентні схеми, тобто такі комбінації С і R, які можуть моделювати електричні параметри біологічних тканин. Розглянемо найпростіші з них.

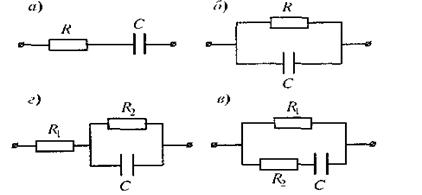
Мал. 2.37.

При послідовному сполученні R і С (мал. 2.37а) схема має суттєві розбіжності з дослідом при пропусканні постійного струму. Якщо 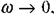то вона чинить нескінченно великий опір постійному струмові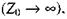що не відповідає дійсності. Якщо ж С і R з'єднати паралельно (мал. 2.37б), то при високих частотах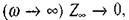що теж не відповідає дійсності. Для біологічних тканин характерне більш складне поєднання ємності й активного опору. Найбільш вдалими є схеми, що приведені на мал. 2.37в,г. При пропусканні через такі схеми високочастотного струму при 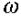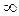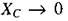_→ ,їх імпеданс асимптотичне наближається до деякої константи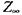(у випадку 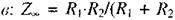), а у випадку 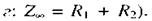Ці схеми з певним наближенням можуть бути еквівалентними електричними схемами біологічних тканин, але ні одна з них не може повністю відтворювати закономірності пропускання електричного струму через біологічні системи.

На мал. 2.38 приведені графіки дисперсії (частотної залежності) імпедансу рослинної тканини: 1 - крива для нормальної здорової тканини; 2 - для нагрітої до протягом 2 хв; 3 - те ж саме протягом 4 хв; 4 - після кип'ятіння в воді протягом 20 хв.

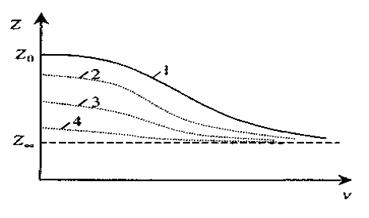
З малюнка видно, що крутизна кривої в міру відмирання тканини зменшується, тобто спостерігається зменшення низькочастотного опору, тоді як при високих частотах імпеданс практично залишається постійним. Причиною є те, що при відмиранні руйнуються мембрани -"живі конденсатори", і нежива біологічна тканина володіє суто омічним опором. Вказані особливості використовуються для оцінки фізіологічного стану об'єктів. Як правило, розраховується коефіцієнт дисперсії К, який дорівнює відношенню імпедансу при низьких частотах до імпедансу при високих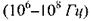частотах:

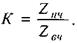(2.80)

У нормальних тканинах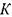залежить від положення організму в еволюційному ряді. Наприклад, коефіцієнт дисперсії печінки ссавців дорівнює приблизно 9-10, печінки жаби - 3-4. При відмиранні тканин вказаний коефіцієнт наближається до одиниці. Критерієм життєздатності є також частотна залежність тангенса кута зсуву фаз між силою струму і напругою. Вона дає уявлення про співвідношення між величинами активного і реактивного опорів:

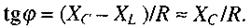
Імпеданс тканин залежить також від їх функціонального стану, і це використовується в діагностиці. Імпеданс кровоносних судин залежить від їх кровонаповнення, а значить і від серцево-судинної діяльності. На цьому базується діагностичний метод, який називають реографією. Реографія вивчає залежність активної складової імпедансу біологічної тканини від її деформації в процесі серцевої діяльності. Отримують реограми серця, головного мозку, магістральних судин, легень тощо. Відповідно до методики Кедрова вважається, що відносна зміна об'єму ділянки кровоносної судини (чи іншої біологічної тканини) 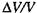прямо пропорційна зміні опору ΔR/R:

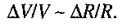
Співвідношення між активною та реактивною складовими опору може змінюватись при зміні фізіологічного стану та деяких патологіях. Наприклад, при запаленні на перших стадіях спостерігається збільшення активного опору тканин. Цей ефект обумовлений тим, що струм низької частоти йде переважно через міжклітинну рідину, яка володіє суто омічним опором. При запаленні клітини набухають і переріз міжклітинних ділянок зменшується, що й призводить до підвищення омічного опору. Ємнісний опір при цьому практично не змінюється, оскільки не змінюється структура клітин. Очевидним є той факт, що за незмінного ємнісного опору збільшення омічного опору свідчить про набухання клітин, а зменшення омічного опору, навпаки, свідчить про зменшення об'єму клітин. Зворотний ефект спостерігається на ранніх стадіях онкологічних захворювань. Перетворення нормальних клітин у ракові супроводжується появою молодих клітин і підвищенням ємнісного опору.

<18 19 202122 23 24 >

Дата добавления: 2020-11-18; просмотров: 487;