Закон Біо-Савара-Лапласа
Напруженість магнітного поля Н, створеного постійним струмом, можна обчислити, використовуючи закон, відкритий експериментальне французькими фізиками Ж.Б. Біо і Ф. Саваром у 1820 р. і сформульований в загальному вигляді П.С. Лапласом.
Виділимо в провіднику зі струмом достатньо малу ділянку dl, яку можна розглядати як вектор, направлений в той же бік, що й струм I.
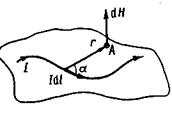
Мал. 2.17.
Добуток 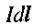 називають елементом струму. Проведемо з елемента струму
називають елементом струму. Проведемо з елемента струму 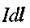 радіус-вектор r в досліджувану точку А (мал. 2.17). Тоді величина напруженості магнітного поля в точці А, створеного даним елементом струму, дорівнює:
радіус-вектор r в досліджувану точку А (мал. 2.17). Тоді величина напруженості магнітного поля в точці А, створеного даним елементом струму, дорівнює:
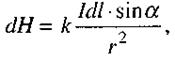 (2.45)
(2.45)
де 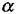 - кут між векторами
- кут між векторами 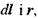 коефіцієнт k залежить від вибору системи одиниць. В системі
коефіцієнт k залежить від вибору системи одиниць. В системі 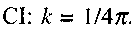 Напрямок dH визначається правилом свердлика: якщо поступальний рух свердлика збігається з напрямком
Напрямок dH визначається правилом свердлика: якщо поступальний рух свердлика збігається з напрямком 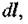 то напрямок
то напрямок 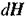 збігається з напрямком обертання рукоятки. Повна напруженість Н магнітного поля, створеного в точці А провідником зі струмом, дорівнює векторній сумі полів, створених всіма елементами струму
збігається з напрямком обертання рукоятки. Повна напруженість Н магнітного поля, створеного в точці А провідником зі струмом, дорівнює векторній сумі полів, створених всіма елементами струму 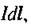 що складають даний провідник. Якщо всі dH мають однаковий напрямок, то сумарна напруженість магнітного поля знаходиться як інтеграл:
що складають даний провідник. Якщо всі dH мають однаковий напрямок, то сумарна напруженість магнітного поля знаходиться як інтеграл:
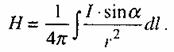 (2.46)
(2.46)
Знайдемо напруженість магнітного поля у вакуумі для деяких простих контурів зі струмом.
Напруженість магнітного поля в центрі колового струму. Коловим називають струм, що протікає по провіднику у формі кола (мал. 2.18). 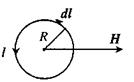
Мал. 2.18.
У цьому випадку всі елементи 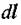 про відника перпендикулярні до радіус- вектора:
про відника перпендикулярні до радіус- вектора: 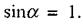 Відстань від усіх елементів провідника до центра кола однакова і дорівнює радіусу кола
Відстань від усіх елементів провідника до центра кола однакова і дорівнює радіусу кола 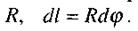 Тому інтегрування в (2.46) дає:
Тому інтегрування в (2.46) дає:
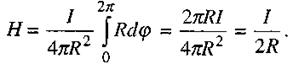 (2.47)
(2.47)
Напрямок вектора Н можна знайти за правилом свердлика і він буде таким, як показано на мал. 2.18 (вектор Н перпендикулярний до площини провідника).
Магнітне поле прямолінійного провідника зі струмом (мал. 2.19) обчислюється за формулою:
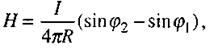
де 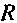 - відстань від провідника зі струмом до даної точки,
- відстань від провідника зі струмом до даної точки, 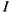 - сила струму в провіднику.
- сила струму в провіднику.
Якщо провідник нескінченно довгий, то 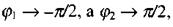 і
і
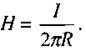 (2.48)
(2.48)
Магнітне поле на осі соленоїда визначається за формулою:
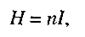 (2.49)
(2.49)
де п - число витків, які припадають на одиницю довжини соленоїда.
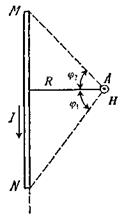
Мал. 2.19.
Величина поля на осі не залежить від радіуса соленоїда R, якщо його
Довжина 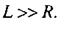
Дата добавления: 2020-11-18; просмотров: 665;











