Рассмотрим поглощение ультразвуковых волн. 8 глава

Так как ввод лекарства сопровождается большим числом самых разнообразных процессов - это перенос лекарства к органам, удаление препарата почками и т. д., то введем следующие допущения:

1. Не рассматривается система органов, через которые проходит лекарство;

2. Не учитываются молекулярные механизмы проходящих процессов – проницаемость веществ и т. д.;

3. Процесс ввода и вывода сводится к скорости.
Рассмотрим законы изменения скорости введения лекарства от времени при различных способах его введения, т. е. изменения c(t) при различных способах введения лекарства (рис. 10.1).

Рис. 14.1. Фармакокинетические модели для различных способов введения лекарственного препарата: однократное (а), попеременное (б) и комбинированное (в) и графики соответствующих им временных зависимостей концентрации лекарственного препарата в организме

1-й способ.Однократное введение лекарственного препарата - инъекция (рис. 14.1, а) (это соответствует случаю, когда пациенту "сделали укол").

Представим себе организм как систему объемом V, после введения в которую лекарственного препарата массой m₀, начинается его удаление из организма. Распределение препарата по объему предполагается равномерным. Скорость удаления р препарата из организма прямо пропорциональна его массе в организме:

p = – km, (14.1)

Скорость изменения массы лекарственного вещества в организме равна скорости его выведения р и, следовательно

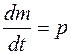(14.2)

Концентрация лекарственного препарата в организме (например, в крови), c = m/V:

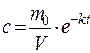(14.3)

или при ,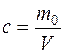

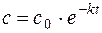. (14.4)

Концентрация лекарственного препарата в крови будет непрерывно снижаться по убывающему экспоненциальному закону (рис. 14.1, а). Таким образом, при однократном способе введения лекарства не удается поддерживать в крови его постоянную концентрацию.

2-й способ.Непрерывное введение препарата с постоянной скоростью – инфузия (рис. 14.1, б) (это соответствует случаю, когда пациенту поставили капельницу). В этом случае изменение массы лекарственного препарата в организме dm/dt определяется не только скоростью его удаления р, но и скоростью введения Q – количеством лекарственного вещества, вводимого в организм за единицу времени:

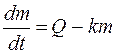(14.5)

Решим это дифференциальное уравнение с учетом, что при t = 0 масса m = 0:

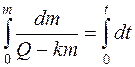(14.6)

Введем новую переменную:

U = Q - km, dU = - kdm, dm = -dU/k, тогда получаем

,

,

,

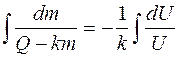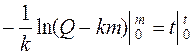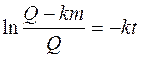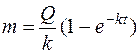, (14.7)

Концентрация лекарства в крови

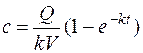. (14.8)

В начальный момент времени, при t = 0, с = 0. При t→ ¥ величина e ^–kt →0 и

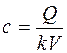. (14.9)

Подобрав скорость введения лекарства Q = kVc_опт, добьемся того, что через некоторое время установится оптимальная концентрация с, необходимая для терапевтического эффекта. При непрерывном способе введения лекарства удается достигнуть заданного результата столько через некоторое время (рис. 14.1, б). Оптимальная концентрация может быть установлена в организме мгновению при сочетании первого и второго способов.

3-й способ.Сочетание непрерывного введения лекарственного препарата (2-й способ) с введением нагрузочной дозы (1-й способ) (рис. 14.1, в) При этом фармакокинетическая модель примет вид:

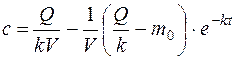(14.10)

График этой зависимости в общем виде представлен на рис. 14.1, в, кривые 1 и 1'. Если выбрать соответствующие скорость введения лекарства

Q = kVс_опт (14.11)

и нагрузочную дозу

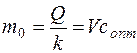, (14.12)

постоянная концентрация с = с_опт устанавливается мгновенно (прямая линия 2, рис. 14.1, в)

Таким образом, фармакокинетическая модель позволяет в пределах выше указанных допущений найти закон изменения концентрации препарата во, времени при различных способах его введения в организм, рассчитать оптимальное соотношение между параметрами ввода и вывода препарата для обеспечения необходимого терапевтического эффекта.

14.2. Модель кровотока при локальном сужении сосудов

Определяющим фактором фильтрационно-реабсорбционных процессов в капиллярах являются гемодинамические параметры кровотока. Однако ряд процессов в сердечно-сосудистой системе может изменить давление и скорость кровотока как в сердечнососудистой системе в целом, так и в отдельных ее частях, тем самым повлиять и на транскапиллярный обмен. Причиной нарушения гемодинамики могут быть изменения просветов сосудов и реологических свойств крови.

Для математического описания системы кровотока и распределения давления и скорости кровотока в ней необходимо упростить систему. Поэтому введем следующие допущения:

1) параметры системы не изменяются во времени;

2) эластичность сосудов не учитывается;

3) не учитываются пульсации давления в различные фазы сердечного цикла, речь будет идти о среднем давлении;

4) течение жидкости ламинарное.

Для исследования поведения системы используем электрические чисто резистивные модели, т.е. аналоговые модели, учитывающие только стационарные режимы и не учитывающие переходные процессы (процессы установления течения). В этом случае течение крови по сосудам будет моделироваться электрическим током в цепи из активных сопротивлений.

Введем эквивалентные величины.

Сила тока во всей цепи I_o = Q_o – объемная скорость кровотока во всей системе.

Падение напряжения U на сопротивлении – это падение давления ΔР вдоль сосуда

Электрический потенциал – давление Р в сечении сосуда.

ЭДС источника е = Р_с – среднее давление в начале аорты.

Сопротивление R = W – гидравлическое сопротивление участков ab или cd (рис. 10.2).

Сопротивление r = w – гидравлическое сопротивление участка be до его сужения.

Сопротивление r = w – гидравлическое сопротивление участка be при его сужении.

Сопротивление r_n = w – гидравлическое сопротивление последующего сосудистого русла.

Сопротивление r₀ = w₀ – гидравлическое сопротивление предшествующего сосудистого русла.

В основу математической модели положены закон Пуазейля, условие неразрывности струи и закон Ома.

1. Сужение крупного сосуда(например, при образовании в нем тромба), рис. 14.2, а.

На рис. 14.2, б приведена эквивалентная электрическая схема.

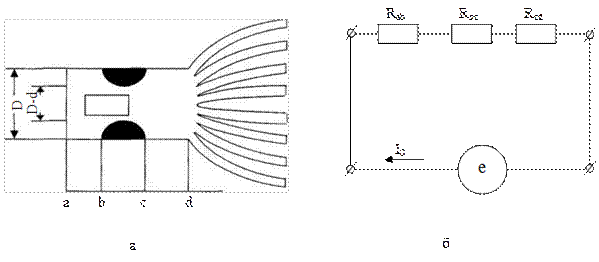
Рис. 14.2. Сужение крупного сосуда (а) и эквивалентная электрическая схема (б). На участке bc произошло сужение сосуда

Поскольку ток в цепи должен оставаться неизменным (по аналогии постоянства кровотока) несмотря на увеличение сопротивления r > R, то должен увеличится потенциал в точке а за счет увеличения ЭДС е.

Исходя из эквивалентной электрической схемы с учетом закона Пуазейля:

Сосуд ab без сужения

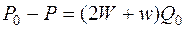. (14.13, а)

Сосуд с сужением

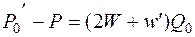(14.13, б)

где Р₀ – давление в т. а, когда сужение отсутствует; Р – давление в точке d; P'₀ давление в т. а при сужении;

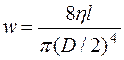(14.14)

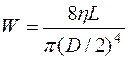(14.15)

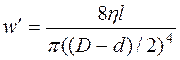(14.16)

где l – длина области сужения (bc), d – изменение диаметра просвета в области сужения, L – длина участка ab и (cd), D – диаметр просвета сосуда в т. а (и d), (D-d) – диаметр просвет в зоне сужения.

Примем условно давление Р на конце данного сосуда ad равным нулю.

Тогда

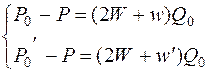(14.17)

Вычитая одно уравнение из другого, получим:

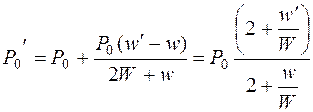(14.18)

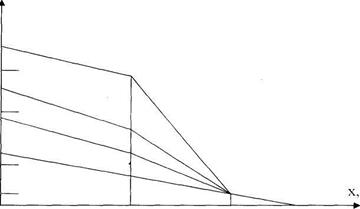
Рис 14.3. Распределение среднего давления вдоль крупного сосуда для различных отношений d/D (для линий 0, 1, 2, 3 отношение d/D равно 0; 0,1; 0,25; 0,4; соответственно)

Найдем падение давления на участках ab, bc, cd

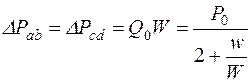(14.19)

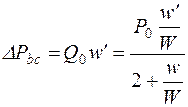(14.20)

Распределение давления вдоль сосуда при сужении участка bс представлено на рис. 14.3. Каждая линия соответствует разному отношению d/D.

Таким образом, на базе данной чисто резистивной модели можно оценить подъем давления крови в левом желудочке сердца при возникновении сужения в крупном сосуде. Ели же кровь не будет выбрасываться под большим давлением из левого желудочка сердца при образовании тромба в крупном сосуде, то давление в конце этого сосуда (в точке d) станет ниже нормы. В результате гидростатическое капиллярное давление Ра понизится, что может привести к нарушению фильтрационно-реабсорбционного равновесия между объемами межклеточной жидкости и плазмы.

2. Сужение одного из мелких сосудов разветвленной системы(возникновение в нем тромба), рис 14.4,а. Число параллельно соединенных сосудов n >10.

На рис. 14.4,б представлена эквивалентная электрическая схема.

Так как общее гидравлическое сопротивление системы неповрежденных сосудов существенно меньше, чем гидравлическое сопротивление сосуда с тромбом , то .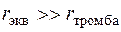

До сужения общее эквивалентное сопротивление участка ad; R_общ =r_с/h (r_с эквивалентно гидравлическому сопротивлению одного сосуда без сужения). После сужения R_общ = r_c /(n-1)

Поскольку 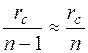при n >10, то можно считать, что общее сопротивление системы не изменилось. Следовательно, ток I₀ в цепи в целом и падение напряжения (P_a – P_d) на участке ad остались прежними. В тоже время произошло перераспределение тока между сопротивлениями (и соответственно кровотока между сосудами: боль шая часть потока потекла в неповрежденные сосуды). Изменился характер падения давления вдоль поврежденного сосуда: в связи с увеличением гидравлического сопротивления увеличилось ΔР вдоль

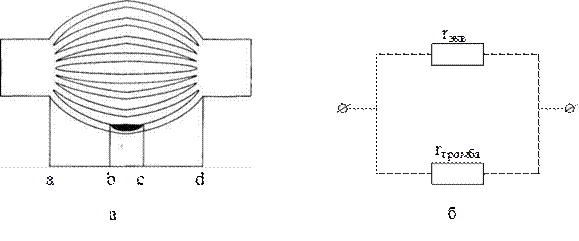
Рис. 14.4 Сужение (образование тромба) одного из мелких сосудов разветвленной системы (а) и эквивалентная электрическая схема (б), r_э – эквивалентное шунтирующее сопротивление, соответствующее общему гидравлическому сопротивлению всех параллельно соединенных сосудов без тромба

суженного участка и уменьшилось ΔР до и после него из-за уменьшения кровотока в поврежденном сосуде. Рассчитаем падение давления и объемную скорость кровотока.