СТАЦИОНАРНОЕ СОСТОЯНИЕ
Стационарным называют такое состояние открытой системы, при котором основные макроскопические параметры системы остаются постоянными. Необходимы различные стационарные состояния от равновесного состояния.
ОТЛИЧИТЕЛЬНЫЕ ПРИЗНАКИ СТАЦИОНАРНОГО И РАВНОВЕСНОГО СОСТОЯНИЯ
| Равновесное | Стационарное |
1. 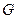 и работоспособность системы минимальные. и работоспособность системы минимальные.
| 1. 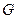 и работоспособность системы постоянны, но не минимальны. и работоспособность системы постоянны, но не минимальны.
|
| 2. Энтропия в системе максимальна. | 1. Энтропия в системе постоянна, за счет равенства продукции и потока энтропии.
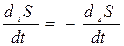
|
| 3. Отсутствие градиентов в системе. | 3. Наличие постоянных градиентов в системе. |
В состоянии равновесия в системе прекращаются все процессы, кроме теплового движения молекул, при этом выравниваются все градиенты.
В стационарном состоянии идут химические реакции, диффузия, перенос ионов и другие процессы, но они так стабилизированы, что состояние системы в целом не изменяется. В стационарном состоянии существуют градиенты между отдельными частями системы, но они сохраняют постоянные значения. Это возможно только при условии, что система из окружающей среды получает вещество и 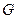 , а отдает продукты реакции и выделяющееся тепло. Термодинамическим условием стационарного состояния является равенство между продукцией энтропии, произведенной организмом, и потоком энтропии, то есть:
, а отдает продукты реакции и выделяющееся тепло. Термодинамическим условием стационарного состояния является равенство между продукцией энтропии, произведенной организмом, и потоком энтропии, то есть:


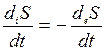 , тогда полное изменение энтропии равно 0
, тогда полное изменение энтропии равно 0 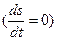 .
.
Термодинамика открытых систем позволяет вскрыть еще одну причину целесообразности стационарного состояния для биологической системы, которая сформулирована в теореме Пригожина:
«В стационарном состоянии продукция энтропии имеет постоянное и минимальное из всех возможных значений, то есть»:

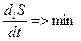
Теорема Пригожина показывает, что в стационарном состоянии диссипация 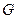 происходит с меньшей скоростью, чем в любых других состояниях, стало быть, в стационарном состоянии
происходит с меньшей скоростью, чем в любых других состояниях, стало быть, в стационарном состоянии  системы расходуется наиболее экономно и поэтому требуется минимальная компенсация ее затрат, то есть, КПД системы в стационарном состоянии максимален.
системы расходуется наиболее экономно и поэтому требуется минимальная компенсация ее затрат, то есть, КПД системы в стационарном состоянии максимален.
Необходимо отметить, что теорема Пригожина справедлива только для таких состояний, которые мало отличаются от стационарных. В этом случае, скорости всех процессов выражаются линейными уравнениями (уравнения 1 порядка).
Теорема Пригожина дает термодинамические критерии эволюции линейным системам, которые формулируются следующим образом:
«Открытая линейная система, если она не находится в стационарном состоянии, будет изменяться до тех пор, пока скорость продукции энтропии в ней не приобретет минимальное значение из всех возможных, то есть, пока величина диссипативная функции не примет минимальное значение.»
Таким образом, второе начало термодинамики для живых организмов можно представить в следующем виде:
I. 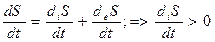 ,
, 
II. 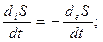
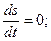
III. 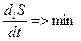
I, II, III - второе начало термодинамики для живых организмов.
КИНЕТИКА БИОФИЗИЧЕСКИХ ПРОЦЕССОВ
УРАВНЕНИЕ ПЕРЕНОСА
Термодинамический подход оказывается плодотворным и при описании кинетических процессов, то есть, скорости их протекания в различных условиях. Термодинамический анализ кинетики дает возможность рассматривать процессы разной природы с единой точки зрения, не вдаваясь в частные механизмы. Это является особенно важным в тех случаях, когда механизм явления очень сложен или вообще непонятен.
При описании любого явления переноса обобщенной координатой 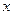 , скорость процесса выражается в виде ее производной по времени
, скорость процесса выражается в виде ее производной по времени 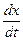 . Во многих случаях скорости процессов прямо пропорциональны соответствующим обобщенным силам -
. Во многих случаях скорости процессов прямо пропорциональны соответствующим обобщенным силам - 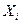 , которая характеризует причины возникновения соответствующего процесса, тогда это можно представить в следующем виде:
, которая характеризует причины возникновения соответствующего процесса, тогда это можно представить в следующем виде:
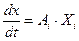
Рассмотрим примеры:
В процессе теплопроводности обобщенной координатой является тепло, а обобщенной силой – градиент температуры:

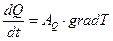 ,
, 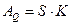
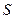 - площадь теплообмена
- площадь теплообмена
 - коэффициент теплопроводности
- коэффициент теплопроводности
Химические реакции:

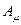 - химическое сродство,
- химическое сродство, 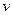 -число молей вещества, вступивших в реакцию за еденицу времени.
-число молей вещества, вступивших в реакцию за еденицу времени.
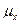 - химический потенциал.
- химический потенциал.
Перенос заряда:
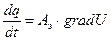 , - закон Ома в дифференциальной форме.
, - закон Ома в дифференциальной форме.
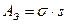 ;
; 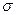 -удельная электропроводность;
-удельная электропроводность; 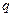 - переносимый заряд; U- разность потенициалов.
- переносимый заряд; U- разность потенициалов.
Диффузионные:
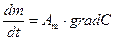 ,
, 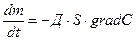
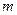 - масса переносимого вещества;
- масса переносимого вещества;
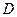 - коэффициент диффузии;
- коэффициент диффузии;
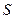 - площадь, через которую идет данный процесс;
- площадь, через которую идет данный процесс;
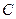 -концентрация.
-концентрация.
В реальных системах практически не бывает изолированных процессов. Они всегда протекают во взаимосвязи, в частности, между одновременно идущими процессами происходит обмен энергией. Такие процессы называют термодинамически сопряженными.
Термодинамическое сопряжение существенно влияет на кинетику биофизических и биохимических процессов, в результате сопряжения, скорость каждого из них будет зависеть не только от своей обобщающей силы, но и от всех обобщающих сил, действующих в системе. С учетом этого, уравнение переноса в общем виде записывается следующим образом:
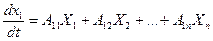

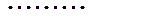
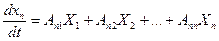
Рассмотрим примеры:
Если в системе (например, в газе) поддерживается одновременно градиент температуры и градиент концентрации, то уравнение переноса записывается в следующем виде:
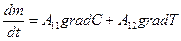

градиент 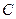 и градиент
и градиент 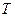 в данном случае являются обобщенными силами.
в данном случае являются обобщенными силами.
Если в какой-то части системы и 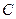 вещества и
вещества и 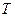 выше, чем в другой, то градиент
выше, чем в другой, то градиент 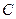 и градиент
и градиент 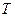 имеют одинаковые знаки, и процессы, происходящие под действием этих градиентов, усиливают друг друга, то есть масса переноса больше, чем в условиях существования только одного градиента. Если же градиенты
имеют одинаковые знаки, и процессы, происходящие под действием этих градиентов, усиливают друг друга, то есть масса переноса больше, чем в условиях существования только одного градиента. Если же градиенты 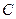 и
и 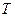 - разнонаправлены, то есть, имеют разные знаки, и при этом
- разнонаправлены, то есть, имеют разные знаки, и при этом 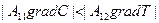 , то
, то 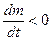 Это означает, что перенос вещества осуществляется против градиента
Это означает, что перенос вещества осуществляется против градиента 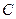 .
.
Транспорт веществ, через клеточные мембраны осуществляется благодаря термодинамическому сопряжению различных процессов, только в тех случаях, когда молекулы транспортного вещества не имеют заряда, химически и осмотически инертны, то процесс массы переноса сводится к простой диффузии (закон Фика):
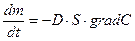
Фактически, такими свойствами в организме обладают только азот и инертные газы, и близко к этому кислород и углекислота. Во всех остальных случаях, например, при транспорте воды, солей, углеводов, жирных кислот и т. д., вместе с концентрационным градиентом действуют и другие градиенты. При транспорте ионов ( 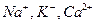 ) по меньшей мере, присутствует три процесса:
) по меньшей мере, присутствует три процесса:
1. Диффузия вещества.
2. Перенос заряда.
3. Химическая реакция (в частности, перенос фосфатной группы с АТФ).
В этой связи, уравнение переноса имеет следующий вид:
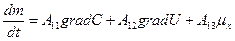
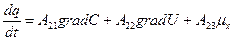
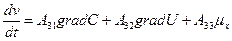
Обобщающими координатами в данной системе уравнений являются m, q и v число молей АТФ, которая обеспечивает энергией активный транспорт ионов, обобщенными силами являются: градиент 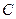 , напряженность электрического поля, химических потенциал (АТФ).
, напряженность электрического поля, химических потенциал (АТФ).
Рассчитав коэффициент 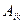 или определив их экспериментально, можно точно знать, в каком направлении идут кинетические процессы по перемещению ионов через биологическую мембрану (БМ).
или определив их экспериментально, можно точно знать, в каком направлении идут кинетические процессы по перемещению ионов через биологическую мембрану (БМ).
Необходимо отметить, что все, выше рассмотренные уравнения, достаточно хорошо описывают процессы, которые не так далеко удалены от состояния равновесия. Так как все уравнения - линейные. Однако, при рассмотрении процессов, происходящих на БМ, приходится иметь дело с большими градиентами, что приводит к большим скоростям процессов. Для описания таких процессов желательно использовать нелинейную термодинамику.
КИНЕТИКА ПРОЦЕССОВ, ИДУЩИХ С ПРЕОДОЛЕНИЕМ
ПОТЕНЦИАЛЬНОГО БАРЬЕРА
Многие реальные процессы в биологической системе идут с преодолением потенциального барьера. Это означает, что начальное и конечное состояние системы разделены некоторым промежуточным состоянием, которое обладает большей энергией.

Чтобы процесс осуществлялся, система вначале должна получить дополнительно энергию 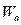 для преодоления потенциального барьера. Величина этой энергии называется высотой потенциального барьера, или энергией активации процесса.
для преодоления потенциального барьера. Величина этой энергии называется высотой потенциального барьера, или энергией активации процесса.
Примером процессов, идущих с преодолением потенциального барьера (ПБ), служат химические и биохимические реакции. Практически все они проходят стадию промежуточного состояния с повышенной энергией. В химии такое состояние называют активированным комплексом.
В реальных телах различные частицы (молекулы, ионы и т. д.) имеют разную энергию. Поэтому в каждом конкретном случае одни частицы способны преодолевать ПБ, а другие - нет. В этой связи скорость процессов, в которых участвуют молекулы данного вещества, будет определяться только числом молекул, которые способны преодолевать ПБ. Такие частицы (молекулы) называются активными. Концентрацию активных частиц можно рассчитать по формуле Больцмана:

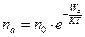
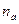 - число активированных частиц;
- число активированных частиц;
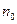 - общее число частиц;
- общее число частиц;
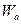 - энергия активации для одного моля вещества.
- энергия активации для одного моля вещества.
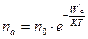
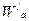 - энергия активации для 1 частицы;
- энергия активации для 1 частицы;
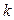 - постоянная Больцмана.
- постоянная Больцмана.
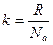 ,
,
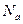 - число Авогадро.
- число Авогадро.
Анализ уравнений Больцмана показывает, что скорость процессов, идущих с преодолением потенциального барьера (ПБ) экспоненциально зависит от температуры. Таким образом, зависят скорости испарения, диффузии, химической реакции и т. д. от температуры. Это имеет важное значение для жизнедеятельности. В этой связи, температурный гомеостазис организма гомойотерных животных является необходимым условием стабильной жизнедеятельности. В противном случае, даже при небольшом отклонении температуры тела от нормы, скорости различных жизненных процессов изменились бы значительно, причем, в неодинаковой степени вследствие различия их энергии активации. Это неизбежно привело бы к нарушению основных функций организма.
Скорость многих химических реакций также определяется энтропией активации. Например, при столкновении двух сложных молекул, которые в принципе взаимодействуют между собой, реакция фактически происходит не всегда. Дело в том, что молекулы взаимодействуют не целиком, а определенными функциональными группами. В этом случае можно сказать, что скорость реакции будет пропорциональна как числу активных частиц, так и вероятности удачных столкновений.
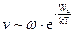
Понятие вероятности в молекулярном движении связано с понятием энтропии:
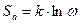
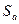 - энтропия активации процесса, следовательно, выражение для скорости процесса примет вид:
- энтропия активации процесса, следовательно, выражение для скорости процесса примет вид:

Скорость реакции можно значительно повысить, если каким-то образом увеличить вероятность удачных столкновений. Для этого необходимо направить навстречу друг другу соответствующие функциональные группы. Именно так действуют ферменты. Ферменты - это биологические катализаторы. Роль ферментов состоит в резком ускорении биохимических реакций. В действии ферментов выделяют два механизма:
одни ферменты в основном снижают энергию активации ( 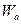 ); другие увеличивают энтропию активации
); другие увеличивают энтропию активации 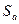 .
.
Дата добавления: 2020-11-18; просмотров: 500;











