Момент сили і момент інерції тіла відносно осі обертання.

Дамо більш строге визначення моменту сили. Моментом сили відносно, будь-якої осі, називається векторМ, який визначається виразом:

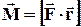, (1.35)

О d=r·sinα

α

F

Рис. 1.23.

r - радіус-вектор, проведений з точки О в точку прикладення сили. На рисунку 1.23 вектор Мперпендикулярний до площини малюнка і спрямований від нас. Напрям вектора моменту сили вибраний так, що обертання навколо точки О у напрямі сили і вектор М утворюють правогвинтову систему.

Модуль вектора М дорівнює добутку величини сили F на плече d, тобто довжину перпендикуляра, опущеного з точки О через яку проходить вісь на напрям сили.

М=F·r·sinα.

Кінетична енергія обертального руху.

Момент інерції.

Якщо тіло рухається поступально, то усі точки його мають одну і ту ж швидкість v. Кінетична енергія будь-якої частини тіла масою m_i, буде рівна m_iv²/2, а кінетична енергія усього тіла визначається сума кінетичних енергій частин тіла.

.

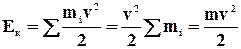Отже, у разі поступального руху тіла його кінетична енергія має такий самий вираз, як і для матеріальної точки.

Якщо тіло обертається біля деякої осі з кутовою швидкістю ω, то лінійні швидкості точок не однакові, вони пропорційні відстаням точок до осі обертання :

.

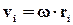Розглянемо суму кінетичних енергій усіх часток тіла, що обертається, :

.

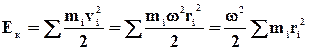Цю формулу для обертальної кінетичної енергії тіла можна привести до виду, аналогічного виразу кінетичної енергії поступального руху, якщо ввести величину І (момент інерції тіла).