Моменти інерції деяких тіл.

Обчислення моментів інерції тіл проводиться за допомогою інтегрального числення. Щоб дати уявлення про хід подібних розрахунків, знайдемо момент інерції стержня відносно перпендикулярної до нього осі (рис. 1.24).

O′

dx

x

O

Рисунок 1.24.

НехайS площа перерізу стержня, ρ-густина матеріалу стержня, l - довжина стержня. Виділимо елементарно малу частину стержня dx, що знаходиться на відстані х від осі обертання. Тоді її масаdm= ρsdx. Оскільки вона знаходиться на відстані х від осі обертання, її момент інерції dI= ρsх²dx. Інтегруємо в межах від 0 до l:

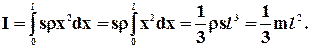(1.40)

У тому випадку, якщо вісь обертання проходить через середину стержня (рис. 1.25)

О' dx

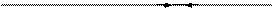
х

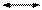О

Рисунок 1.25.

інтегрування проводимо в межах від 0 доl/2, а кінцевий результат подвоюємо

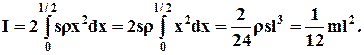(1.41)

Приведемо моменти інерції деяких однорідних тіл рис 1.26.

А б в г

Рисунок 1.26.

Момент інерції круглого диска або суцільного циліндра, радіусу R відносно осі, що проходить через його центр і перпендикулярної до його площини (рис.1.26 а).

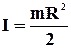. (1.42)

Момент інерції тонкого круглого кільця радіусу R, або тонкостінного циліндра відносно осі, що проходить через його центр і перпендикулярної до його площини (рис.1.26 б).

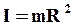. (1.43)

Момент інерції кулі, радіусу R відносно осі, яка співпадає ї з її діаметром
(рис.1.26 в).

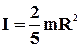. (1.44)

Момент інерції тонкого стержня, завдовжки l відносно осі, що проходить через його центр і перпендикулярної до стержня (рис.1.26 г).

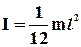. (1.45)

Теорема Штейнера.

У тому випадку, коли вісь обертання не співпадає з віссю симетрії, знаходити момент інерції можна за допомогою теореми Штейнера :

Момент інерції I відносно довільної осі дорівнює сумі моментів інерції I₀ відносно осі, паралельній даній і проходить через центр маси тіла, і добутку маси тіла на квадрат відстані а між осями.

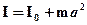. (1.46)