Момент імпульсу. Закон збереження моменту імпульсу

Зважаючи на можливість зміни моменту інерції тіла під час обертання, основне рівняння динаміки обертального руху запишемо у такому вигляді:

.

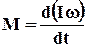З'ясуємо фізичний зміст величини Iω. При обертальному русі тіла кожна його частка з масою m описує коло деякого радіусуr, маючи при цьому швидкість v (рис. 1.28). Добуток маси на швидкість mv - є імпульс цієї частки. Добуток імпульсу частки на найкоротшу відстань до осі обертання, тобто величина mvr, називається моментом імпульсу L частки відносно осі обертання.

mv

r

O

Рисунок.1.28.

Узявши суму моментів імпульсу усіх часток, що становлять тіло, отримаємо момент імпульсу усього тіла.

.

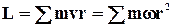Виносячи за знак суми загальний для усіх точок множникωі враховуючи, щоΣmr² є моментом інерції тіла отримаємо:

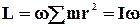. (1.48)

Таким чином, момент імпульсу твердого тіла відносно нерухомої осі дорівнює добутку моменту інерції на кутову швидкість.

Момент імпульсу розглядається як вектор, спрямований по осі обертання і співпадаючий по напряму з вектором кутової швидкості.

Тоді рівняння динаміки обертального руху можна записати у такому вигляді:

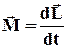. (1.49)

Розглянемо окремий випадок, коли на тіло не діють зовнішні сили або вони такі, що їх рівнодійний момент відносно осі обертання дорівнює нулю.

Але, якщо зміна моменту імпульсу дорівнює нулю, сам момент імпульсу залишається постійний.

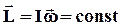. (1.50)

Отже, якщо на тіло не діють зовнішні сили (чи результуючий момент їх відносно осі обертання дорівнює нулю), то момент імпульсу тіла відносно осі обертання залишається постійним. Цей закон носить назву закону збереження моменту імпульсу відносно осі обертання.

Наведемо декілька прикладів, що ілюструють закон збереження моменту імпульсу. Гімнаст, виконуючи сальто, підтискає до тулуба руки і ноги. Цим він зменшує свій момент інерції, а оскільки добуток Iωповинен залишатися незмінним, то кутова швидкість зростає, і в короткий проміжок часу, поки гімнаст знаходиться в повітрі, він устигає зробити один або декілька оборотів.

Кулька, прив'язана до нитки, що намотується на палицю; у міру того як зменшується довжина нитки, зменшується момент інерції кульки, отже, зростає кутова швидкість.

Зіставляючи рівняння, що характеризують закони динаміки обертального руху і порівнюючи їх із законами прямолінійного поступального руху, можна помітити, що формули, що визначають обертальний рух відносно нерухомої осі, аналогічні формулам для прямолінійного поступального руху.

У таблиці 1.3 зіставлені основні величини і рівняння, що визначають ці рухи.

Таблиця 1.3

Поступальний рух

Обертальний рух

Маса ··············································· m Шлях ············································· S Швидкість·········································· v Прискорення... .................................................. a Імпульс·············································p=mv Сила... ............................................................... F Основне рівняння ………………….. 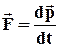Робота... ..............................................dA=F·dS Кінетична енергія... ………..

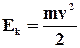
I·····························Момент інерції φ································Кут повороту ω··························Кутова швидкість ε······················Кутове прискорення L=Iω ·····················Момент імпульсу M ···························Момент сили 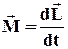·············Основне рівняння dA=Mdφ ························Робота 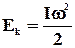···· ··· ·Кінетична енергія

Завдання:

1. Що називається моментом сили і моментом інерції тіла відносно нерухомої осі. Вкажіть одиниці виміру моменту сили, моменту інерції.

2. Що таке момент імпульсу матеріальної точки? Твердого тіла? Як визначається напрям моменту імпульсу?

3. Вивести формули моментів інерції обруча, суцільного циліндра, кулі.

4. У чому полягає фізична суть закону збереження моменту імпульсу? Наведіть приклади використання закону збереження моменту імпульсу.

5. Через нерухомий блок у вигляді суцільного циліндра масою 5 кг перекинутий шнур, до якого прив'язані вантажі масою 4 і 3 кг Визначити прискорення вантажів і силу натягнення шнура з боку кожного вантажу.(1 м/с², 36 Н, 30 Н)

6. З похилої площини почали одночасно скочуватися без ковзання суцільний циліндр і куля . Визначити відношення швидкостей циліндра і кулі у кінці похилої площини.
(v_ц / v_к = 1,035)

7. Швидкість обертання маховика, момент інерції якого 2,5 кг·м², в результаті гальмування рівномірно зменшилася за 1 хвилину від 300 об/хв до 150 об/хв. Визначити момент сили гальмування, кутове прискорення, роботу сили гальмування.
(0,65 Н·м, 0,26 Рад/с², 918 Дж).

8. Людина масою 70 кг стоїть на краю горизонтальної платформи масою 100 кг. Платформа обертається з частотою 10 об/хв. Вважаючи платформу однорідним диском, а людину точковою масою визначити з якою частотою почне обертатися платформа, якщо людина переходить в її центр?. (24 об/хв).

Розділ 2