Геометрична сума внутрішніх сил механічної системи дорівнює нулю.

Напишемо рівняння, що виражає другий закон Ньютона, для кожного з n тіл механічної системи. Рівнодійну прикладених до цього тіла внутрішніх сил позначимо вектором 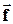, рівнодійну прикладених до нього зовнішніх сил - вектором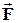

.........

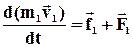
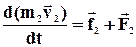
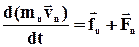
Складемо за правилом складання вектори, що стоять в лівих і правих частинах рівнянь.

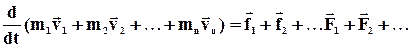
В правій частині рівняння знаходиться сума внутрішніх сил,але вона дорівнює нулю, оскільки усі ці сили попарно рівні за величиною і протилежні по напряму. Залишаються лише зовнішні сили. Тому отримуємо:

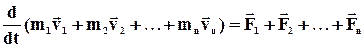
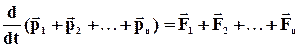
За відсутності зовнішніх сил виходить, що

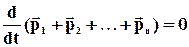, чи ,

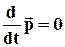де 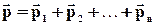- результуючий імпульс системи.

Звідси витікає, що імпульс не повинен мінятися з часом.

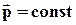. (1.25)

Це надзвичайно важливий результат: якщо до системи не прикладені зовнішні сили, повний імпульс системи зберігається з часом. Таке формулювання виражає закон збереження імпульсу. Цей закон виконується не лише в класичній фізиці, але і в явищах, що вивчаються в квантовій механіці.

Закон збереження імпульсу у багатьох випадках дозволяє знаходити швидкості взаємодіючих тіл навіть тоді, коли значення діючих сил невідомі. Розглянемо деякі приклади.

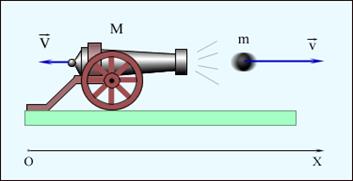
При стрільбі з гармати виникає віддача - снаряд рухається вперед, а гармата - відкочується назад. Снаряд і гармата - два взаємодіючі тіла. Швидкість, яку отримує гармата при віддачі, залежить тільки від швидкості снаряда і відношення мас (рис. 1.15а). Якщо швидкості гармати і снаряда позначити через V і v, а їх маси через М і m, то на підставі закону збереження імпульсу можна записати

.

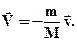Рисунок .1.15а. Рисунок.1.15 б.

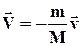На принципі віддачі заснований реактивний рух. У ракеті при згоранні палива гази, нагріті до високої температури, викидаються з сопла з великою швидкістю відносно ракети (рис 1.15 б). Позначимо масу викинутих газів через m, а масу ракети після витікання газів через M. Тоді для замкнутої системи "Ракета + гази" можна записати на підставі закону збереження імпульсу (по аналогії із завданням про постріл з гармати) :

.

де V - швидкість ракети після витікання газів, v - швидкість газів.

Тут передбачалося, що початкова швидкість ракети дорівнювала нулю.

Отримана формула для швидкості ракети справедлива лише за умови, що уся маса згорілого палива викидається з ракети одночасно. Насправді витікання відбувається поступово впродовж усього часу прискореного руху ракети. Кожна наступна порція газу викидається з ракети, яка вже придбала деяку швидкість. Для отримання точної формули процес витікання газу з сопла ракети треба розглядати детальніше.