Роботу вимірюють добутком сили, діючої на тіло у напрямі переміщення, на величину переміщення точки прикладення сили. Енергію вимірюють роботою, яку може виконати тіло.
У механіці розрізняють енергії кінетичну і потенціальну. Під кінетичною енергією розуміють енергію механічного руху, вимірювану роботою, яку тіло здатне виконати при загальмовуванні до повної зупинки. Під потенціальною енергією розуміють енергію прихованих форм руху, вимірювану роботою, яку тіло здатне виконати, коли його переміщають без зміни швидкості з однієї точки простору в іншу. Потенціальну енергію інакше називають енергією взаємодії.
Кожна фізична форма руху характеризується тим або іншим видом енергії. Коли ми вивчаємо тепловий рух, то маємо справу з внутрішньою енергією. У електростатиці і магнетизмі ми стикаємося з електричною і магнітною енергією.
За приведеним вище визначенням, робота A, виконана силою F, спрямованою під кутом α до переміщення, на шляху S дорівнює:
A=F S cosα .(1.26)
Таким чином, робота постійної сили дорівнює добутку модуля вектора сили на модуль вектора переміщення і на косинус кута між цими векторами.
Сила, спрямована перпендикулярно до переміщення (α=90˚), не виконує роботи. З цієї точки зору розкладання сили на тангенціальну і доцентрову складові набуває особливий фізичний зміст; дія доцентрової сили позначається тільки в зміні напряму руху, тоді як тангенціальна сила виконує роботу, що проявляється або із збільшенням швидкості руху, або в подоланні сил опору.
За одиницю роботи приймають роботу, здійснену силою 1 Н, на шляху, рівному 1 м Одиницю роботи називають джоулем (Дж), на честь англійського вченого Джеймса Прескотта Джоуля, який провів важливі для науки досліди по виміру роботи. 1 Дж = 1Н·1 м.
Якщо проекція сили на напрям переміщення не залишається постійною під час руху, для обчислення роботи слід розбити шлях S на елементарні ділянки ds, узявши їх такими малими, щоб за час проходження тілом такої ділянки величину Fs можна було вважати майже незмінною. Тоді робота сили на кожній елементарній ділянці приблизно дорівнює:
dA=Fs dS.
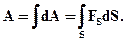 Повна робота визначається інтегралом:
Повна робота визначається інтегралом:
(1.27)
Графічно робота визначається по площі криволінійної фігури під графіком Fs(рис.1.16).
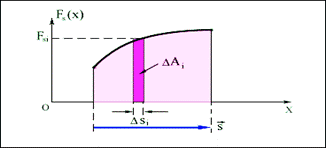 |
Рисунок. 1.16.
Прикладом сили, модуль якої залежить від координати, може служити пружна сила пружини. Для того, щоб розтягнути пружину, до неї треба прикласти зовнішню силу, модуль якої пропорційний подовженню пружини x (рис 1.17).
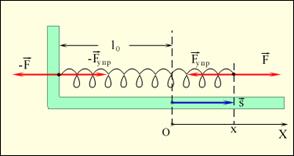 | 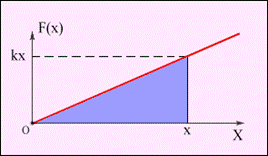 |
Рисунок. 1.17. Рисунок.1.18.
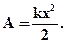 Напрям пружної сили співпадає з напрямом переміщення. F=Fs=kx, k - жорсткість пружини. Залежність модуля зовнішньої сили від координати x зображається на графіці прямою лінією (рис.1.18). По площі трикутника на (рис 1.18) можна визначити роботу, здійснену зовнішньою силою, прикладеною до правого вільного кінця пружини :
Напрям пружної сили співпадає з напрямом переміщення. F=Fs=kx, k - жорсткість пружини. Залежність модуля зовнішньої сили від координати x зображається на графіці прямою лінією (рис.1.18). По площі трикутника на (рис 1.18) можна визначити роботу, здійснену зовнішньою силою, прикладеною до правого вільного кінця пружини :
.
Тією ж формулою виражається робота, здійснена зовнішньою силою при стискуванні пружини.
Якщо на тіло діє декілька сил, то загальна робота усіх сил дорівнює сумі робіт, що здійснюються окремими силами і дорівнює роботі рівнодійною прикладених сил(рис. 1.19)..
Робота рівнодійної сили. 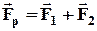 , дорівнює:
, дорівнює:
А=F1Scos α1 + F2Scos α2 = F1sS + F2sS = FрScos α.
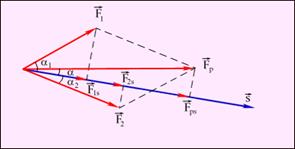
Рисунок 1.19.
Дата добавления: 2020-10-25; просмотров: 607;











