Internal strain energy in torsion

Under torsion the torques make the work owing to the section twist to which they are applied to be. This work is used to store the strain energy which is numerically equal to the internal force work.

The work of the statically applied torque is equal to half the product of the finite moment and the finite angle of the twist:

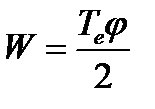(4.16)

The internal force work of the negative sign is numerically equal to the strain energy

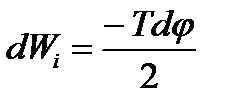(4.17)

where T is the twisting moment, 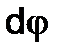is the twist angle of the element which has the length dz.

But according to the formula (4.17) we have

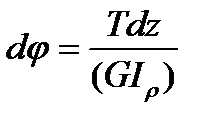
Hence

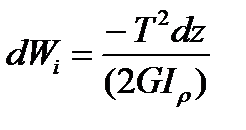(4.18)

Integrating the expression of the elemental work along the bar length 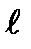we receive the total internal force work:

.

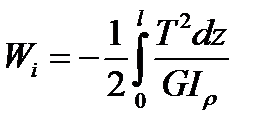To calculate the strain energy which is equal to the internal force work of the same magnitude but the inverse sign we have

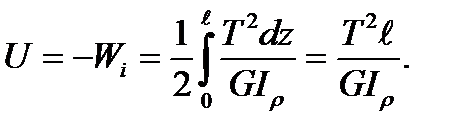(4.19)

BENDING OF bars

The bars are often subject to the action of the transverse load or the external couples (Fig. 5.1). Under that the bending moments arise at the bar cross sections, i.e. the resisting moments which have the action plane perpendicular to the bar cross section plane (in Russian literature the term “bending moment” means the internal stress).

Under the action of this load the bar axis is curved. The pointed load type is called bending and bar subjecting bending – beams.

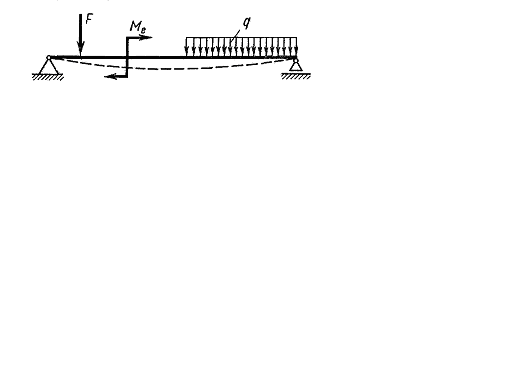
Fig. 5.1.