Combined torsion and compression

In this case two internal stresses arise at the bar cross section: the twisting moment and the normal force (tension and compression)

For the bar of the circular section in torsion the maximum shearing stresses take place at the points of the section contour 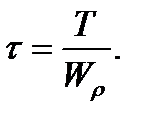The normal stresses 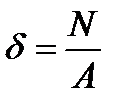arise at all points of the cross section in torsion.

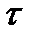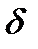Now, like in the case of combined torsion and bending stresses, it is necessary to determine the principal stresses and to apply the corresponding strength hypothesis. As a result we shall receive the formula (7.29) (according to the strength hypothesis) or (7.34) (according to the fourth hypothesis) for the equivalent stresses. The values and should be put into the above given formulas.

Finally we shall receive the strength condition for the combined torsion and tension (compression):

a) according to the third strength hypothesis

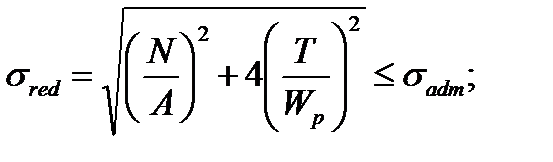(7.37)

c) according to the fourth strength hypothesis

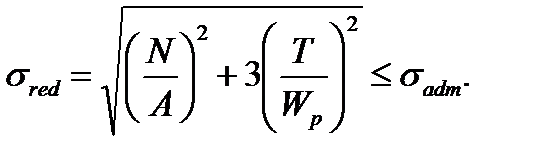(7.38)

It is recommended to prefer the formula (7.37) as the fourth hypothesis for the plastic materials accords with experiments and leads to a more economical decision.