Strain energy in bending

Under bending the work done by the external forces is to change the strain energy of the deformed bar. The work of the external moment M_e can be calculated by the formula

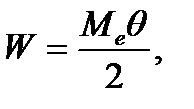
where 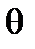is the section rotation angle at the point of the application moment.

The unit work of the bending moment can be found by the formula:

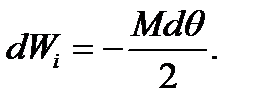(5.21)

The total work of the bending moment of the beam long L is

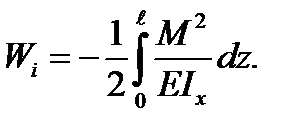(5.22)

In a general case of bending there arise the shearing forces apart from the bending moment at the beam cross section.

However, the strain energy of the shear corresponding to the work of the shearing force is not large – as the research work shows – and it is often neglected.

Therefore the formula (5.23) is useful both for the pure and general case of bending.

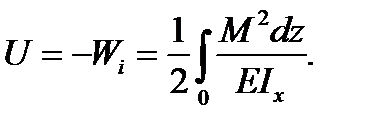(5.23)

5.10. Betty^’s reciprocal theorem. Reciprocal displacement theorem

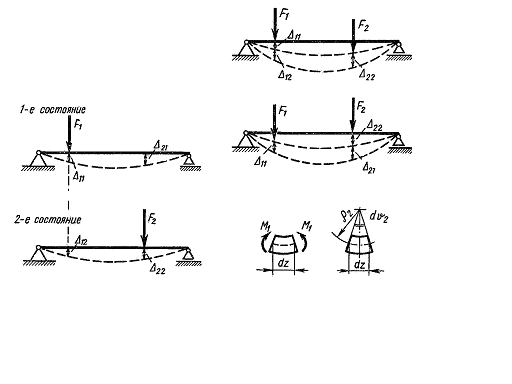
Let us prove the theorem having an important application, that is Betti^’s reciprocal theorem. For this consider a deformed line system in two different conditions corresponding to two different loads (Fig. 5.11). For the simplest case to be considered take a simple beam loaded by the simplest load in two conditions (in one concentrated force). The load, the internal forces and deformations corresponding to these conditions are noted by indexes 1 and 2.

The first system state is represented in Fig. 5.11 a and the second in Fig. 5.11 b.

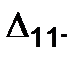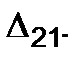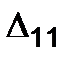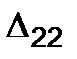The displacement in the load direction for the first state of this load is denoted by The displacement in the load direction for the second state caused by the load action of the first state is denoted by The designations of the displacement of the second state are given in Fig. 5.11 b. The displacements containing two similar indices, for example and are called principal and the displacements of kind 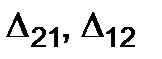and the like are secondary. Now prove Betti^’s reciprocal theorem, namely: the external force work of the first state on the displacement of the second state is equal to the force work of the second state on the displacement caused by the forces of the first state.

the first state

the second state

Fig. 5.11. Fig. 5.12.

To prove the theorem let us load the beam by forces F₁ and F₂ applying them in a different sequence.

1. To start let us apply the load F₁ and then apply the force F₂ to the deformed beam (Fig. 5.12 a).

2. Calculate the work done by the external forces in this case.

The work done by the force F₁ on its displacement 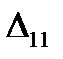caused by this force is 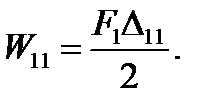The work done by the force F₂ on its displacement 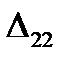is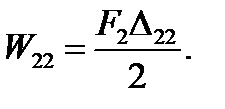

The additional work of the force F₁ on the displacement 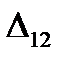caused by the force is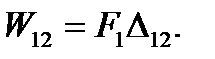

Pay attention to that under the calculation of W₁₂the multiplier 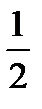is missing because the force F on the displacement 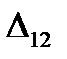fulfils the work, being constant.

The total work done by the external forces under the first way loading (consequence) is

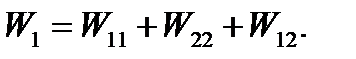(5.24)

The actual work W₁₂ done by the force on the displacement caused by the other force (forces) is called additional work. But this work may not be done, and it can be considered only as virtual, i.e. which will be done if the system is loaded by two loads simultaneously. That work is called the virtual (possible) work.

Under further computations we will not differentiate between the additional and virtual works.

2. Load now the beam in another sequence: first let us apply the force F₂ and then the force F₁ (Fig. 5.12 b). The work done by the force F₂ on its displacement 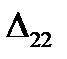is

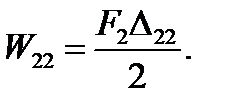(5.25)

The work done by the force F₁ on its displacement 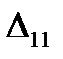is

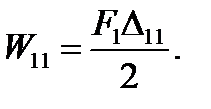(5.26)

The work done the force F₂ on the displacement 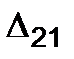is

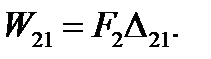(5.27)

The total work in the second way of loading is

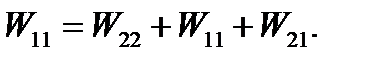(5.28)

But the force work does not depend on the order of their application. Hence, W₁=W₁₁, from where we get

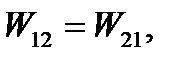(5.29)

or for the case considered

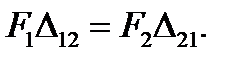(5.30)

This proves the above formulated theorem about the reciprocal virtual works of the external forces. We have proved it by the example of the concentrated external loads. But the theorem will also be correct for any external load: concentrated, distributed, external moments. It should be kept in mind that the moments work is calculated in this case not on the line but angle displacements.

Analogously there can also be proved the reciprocal virtual work of the internal forces:

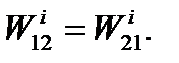(5.31)

Using the energy preservation law it can be shown that the additional work of the external forces is equal to the absolute value of the additional work of the internal forces: 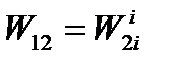and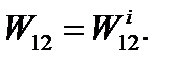

It follows that

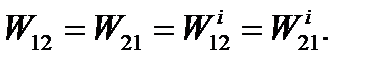(5.32)

These relations will be used further for the substantiation of the general method of displacements determining (Mohr^’s method). The important reciprocal displacement theorem follows from Betti^’s reciprocal theorem as the special case.

Taking F₁=F₂=1 we get

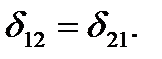(5.33)

Here the displacements caused by the forces are equal to the unit and they are denoted by 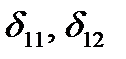and so on.

The displacement of the application point of the unit force to its direction caused by a second unit force is equal to the displacement of the application point of the second unit force in the direction of the latter caused by the action of the first unit force.

5.11. Determining displacements by Mohr^’s method

Consider now the general method of determining the displacements that is suitable for any linear deformed system under any load. The method was proposed by an outstanding German scientist O. Mohr.

For example, you have to determine the vertical displacement of the bar point B as presented in Fig. 5.13 a. Denote the given (load) state by f. Choose the auxiliary state of the same beam with the unit (dimensionless) force acting at the point B to the direction of the sought displacement. Denote the auxiliary state by k (Fig. 5.13 b).

Determine the work of the external and internal forces of the auxiliary state on the displacements caused by the force action of the load state.

The work of the external forces is equal to the product of the unit force and the sought displacement :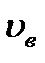

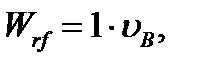(5.34)

and the work of the internal force is equal to the integral:

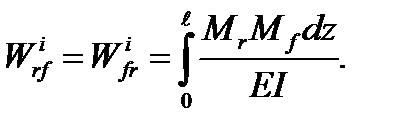(5.35)

But 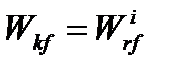or 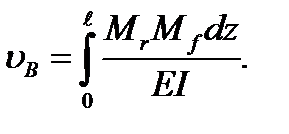(5.36)

a)   b)

state f

state k

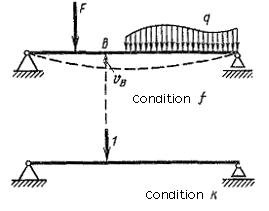
Fig. 5.13.

This formula is in fact Mohr^’s formula (Mohr^’s integral) which gives the possibility to determine the displacement at any point of the linear deforming system.

The subintegral product M_kM_f in this formula is positive if both the bending moments have the same sign; and it is negative if M_k and M_f have different signs.

If we determine the angle displacement at the point B, we should apply at the point B a moment equal unit (dimensionless) for the state k.

Denoting by Δ any displacement (linear or angular) we write Mohr^’s formula (integral) in the following form

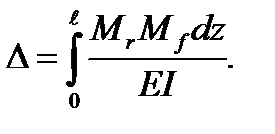(5.37)

In a general case the expressions M_k, M_f can be different for different beam regions or for elastic system in general. Therefore a more general formula must be used.

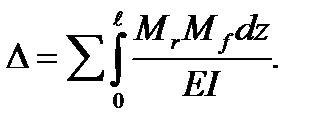(5.38)

If the system bars work in bending or tension, this formula must be used

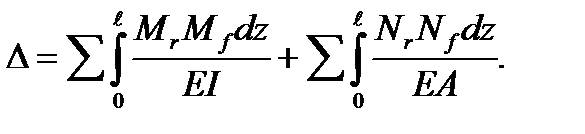(5.39)

In a particular case when the bars work only in tension or compression to determine the displacements, we have the formula

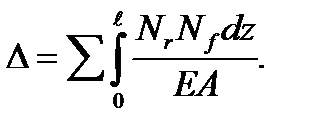(5.40)

In this formula the product N_kN_f is positive if both stresses are elongated or compressed.

In the frame calculations when the bars work simultaneously both in bending and tension (compression) in usual cases – as the comparison calculations show – the displacement can be determined only by considering the bending moments because the shearing force influence is very small. For the same reason in usual cases the shearing force influence may not be taken into account.

If the states f and k are the same, we get:

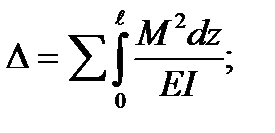
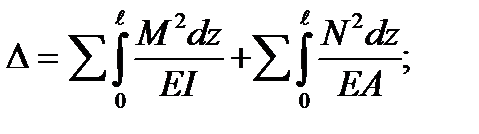(5.41)

Strengtn theory