The stress characterizes the intensity of internal forces acting over the section i.e. the load per a unit area.
Let us consider any arbitrary loading beam and apply to it the method of sections (Fig.1.3)
Let us remove from the section an infinitely small element of the area dA. Because the element is small, it can be assumed that within its limits the internal forces applied in different points are equal to the value and direction, hence, they form a system of parallel forces. The resultant of this system is denoted by dF. After dividing dF into the element area dA we can determine the internal forces intensity i.e. the stress p at the points of the element area dA and we get 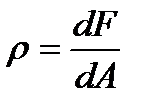 adm
adm
Thus, the stress is the internal force acting over a unit area of the section. The stress is the vector value.
The stress unit is:
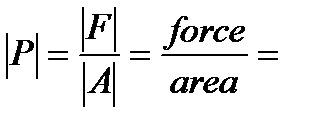 Newton per square meter =
Newton per square meter = 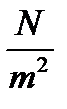 = Pascal (Pa).
= Pascal (Pa).
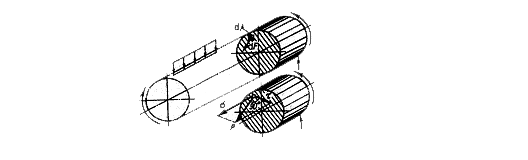
Fig.1.3.
Since this stress unit is very small, we shall apply a bigger divisible unit, namely megapascal (MPa):
1 MPa =10 6 Pа = 1 N/mm2.
Let us decompose the stress vector P into two components: 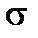 - perpendicular to the section plane and
- perpendicular to the section plane and 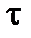 -lying at the section plane (see Fig.1.3). These components are called as follows:
-lying at the section plane (see Fig.1.3). These components are called as follows: 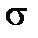 is the normal stress, t is the shearing stress.
is the normal stress, t is the shearing stress.
Since the angle between the normal and shearing stress is always 900, then the absolute value of the resultant stress p is determined by the formula 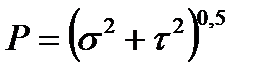
Дата добавления: 2020-10-25; просмотров: 649;











