Определение коэффициента запаса прочности при асимметричном цикле напряжений

Для расчетов при асимметричном цикле напряжений принимают упрощенную диаграмму CML предельных напряжений образца (см. рис. 11.6 и 11.15) Учитывая концентрацию напряжений, влияние абсолютных размеров поперечного сечения детали, состояние поверхности, строят диаграмму предельных напряжений детали. При этом в соответствии с данными опытов влияние перечисленных факторов относят только к переменной составляющей цикла, т. е. к амплитуде 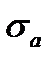. Предельная амплитуда напряжений для образца согласно формуле (11.5),

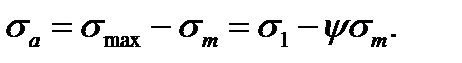(11.18)

Предельная амплитуда напряжений для детали согласно сказанному выше равна

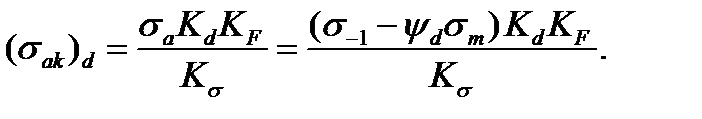(11.19)

Уравнение линии предельных напряжений EN (рис. 11.15) для детали получит вид

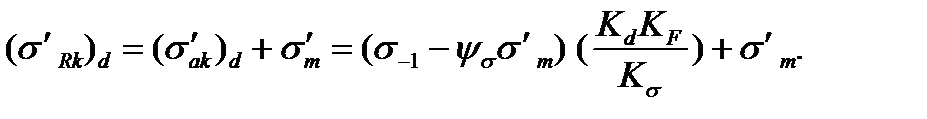(11.20)

Здесь штрихами обозначены текущие координаты.

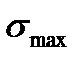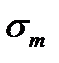Вычислим теперь коэффициент запаса прочности детали при действии переменных напряжений и , (точка R диаграммы, рис. 11.15).

Предположим, что при увеличении нагрузки на деталь отношение 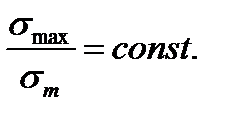Такое нагружение называется простым.

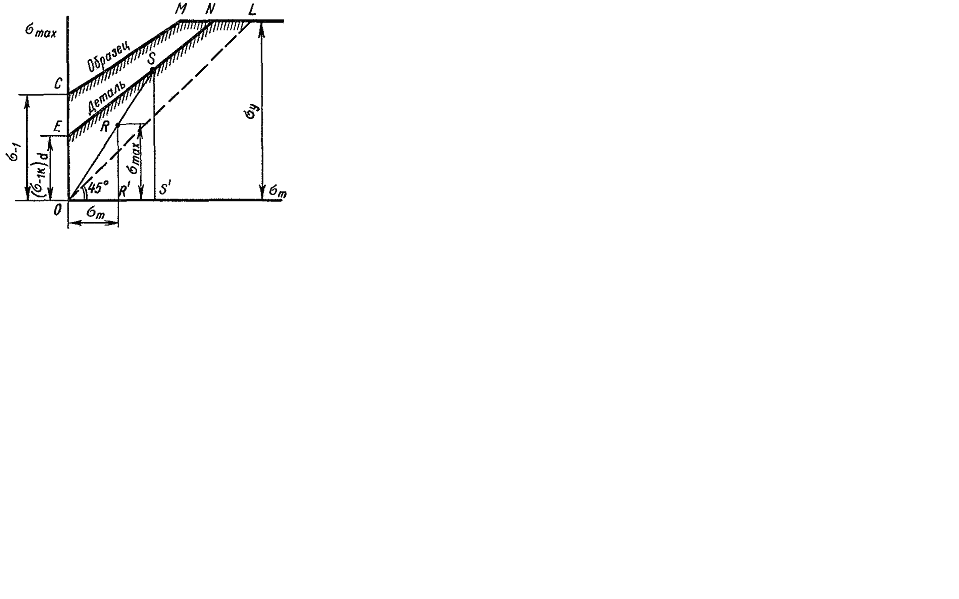
Рис. 11.15.

В этом случае предельной точкой, соответствующей разрушению, является точка S.

Коэффициент запаса прочности равен отношению отрезков SS' и RR':

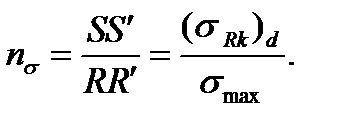(11.21)

Величину ( 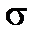_Rk )_d (ординату точки S) найдем в результате совместного решения уравнений линии EN и линии OS. Уравнение линии OS имеет вид

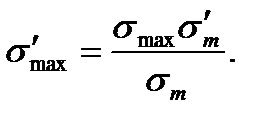(11.22)

(штрихами обозначены текущие координаты).

Приравняв правые части формул (11.20) и (11.22), получим

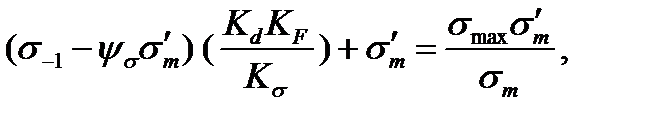(11.23)

откуда

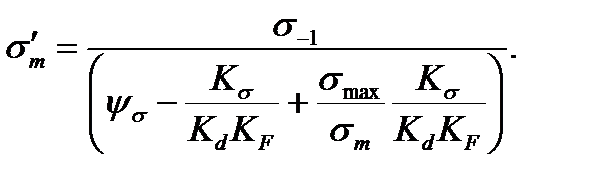(11.24)

Подставив значение 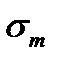в формулу (11.20) или (11.22), найдем ординату точкиS.

Величину ( _Rk)_d (ординату точки S) найдем в результате совместного решения уравнений линии EN и линии OS. Уравнение линии OS имеет вид

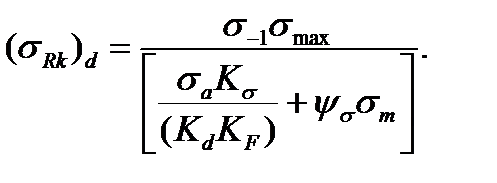(11.25)

Следовательно, на основании формулы (11.21) получается следующая окончательная зависимость для определения коэффициента запаса прочности:

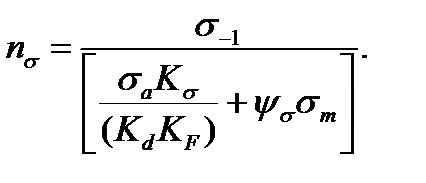(11.26)

Аналогично, при кручении

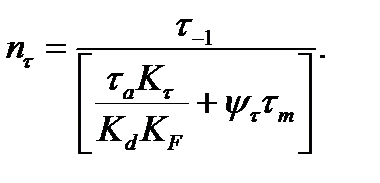(11.27)

При сложном напряженном состоянии, возникающем, например, при кручении с изгибом, коэффициент запаса прочности вычисляют по формуле:

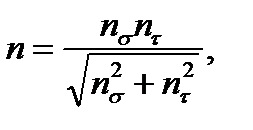(11.28)

а значения 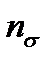, и 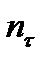- по формулам (11.26) и (11.29).

Кроме коэффициента запаса прочности по сопротивлению усталости необходимо вычислять коэффициент запаса по сопротивлению пластическим деформациям, так как точка s может оказаться выше линии ML. Коэффициент запаса прочности по сопротивлению пластическим деформациям вычисляется по формулам

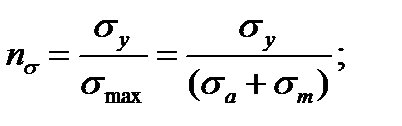(11.29)

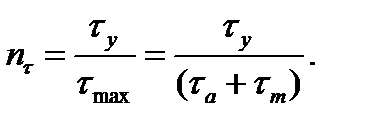(11.30)

Расчетным (действительным) является меньший из коэффициентов запаса, вычисляемых по формуле (11.26) или (11.29) либо при кручении соответственно по формуле (11.27) или (11.30). В случае расчета на изгиб с кручением в формулу для определения общего коэффициента запаса прочности следует подставлять меньшие из значений n_σ, и n_t, вычисляемые, как указано выше.