Диаграммы предельных напряжений и амплитуд цикла
Для определения предела выносливости при действии напряжений с асимметричными циклами строятся диаграммы различных типов. Наиболее распространенными из них являются:
1) диаграмма предельных напряжений цикла в координатах 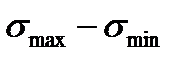 ;
;
2) диаграмма предельных амплитуд цикла в координатах 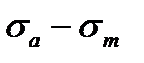 .
.
Рассмотрим эти диаграммы. В диаграмме первого типа предельное напряжение цикла, соответствующее пределу выносливости, откладывается по вертикали, среднее напряжение - по горизонтальной оси (рис. 11.6).
Вначале на ось  наносится точка С, ордината которой представляет собой предел выносливости при симметричном, цикле
наносится точка С, ордината которой представляет собой предел выносливости при симметричном, цикле 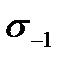 (при симметричном цикле среднее напряжение равно нулю). Затем экспериментально определяют предел выносливости для какой-нибудь асимметричной нагрузки, например для пульсационной, у которой максимальное напряжение всегда в два раза больше среднего. На диаграмму нанесем точку Р, ордината которой представляет собой предел выносливости для от пульсационного цикла
(при симметричном цикле среднее напряжение равно нулю). Затем экспериментально определяют предел выносливости для какой-нибудь асимметричной нагрузки, например для пульсационной, у которой максимальное напряжение всегда в два раза больше среднего. На диаграмму нанесем точку Р, ордината которой представляет собой предел выносливости для от пульсационного цикла 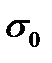 . Для многих материалов значения
. Для многих материалов значения 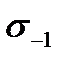 и –
и – 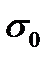 определены и приводятся в справочниках.
определены и приводятся в справочниках.
Аналогично опытным путем определяют предел выносливости для асимметричных циклов с другими параметрами.
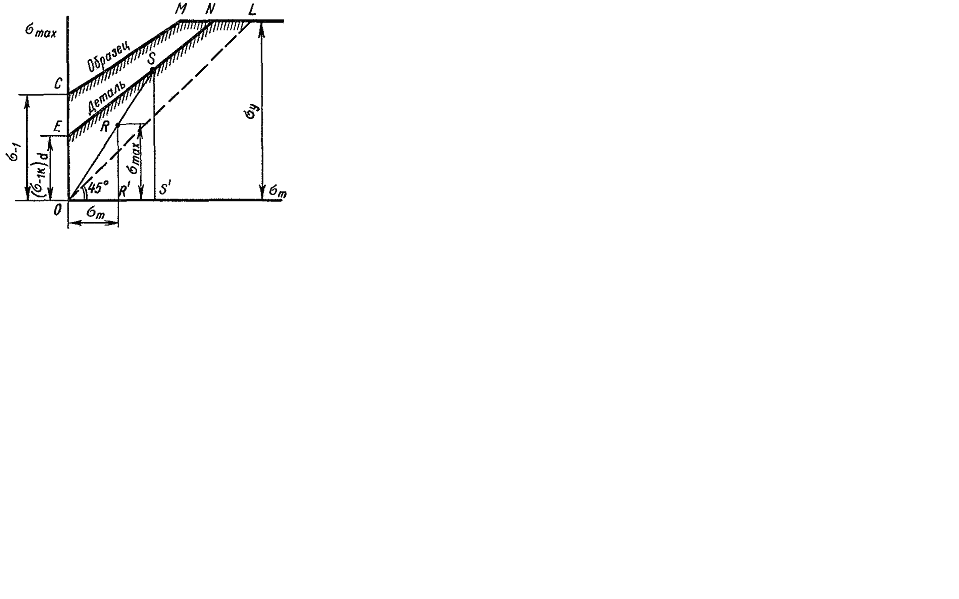
Рис. 11.6.
Рис. 11.6.
Результаты наносят на диаграмму в виде точек А, В и т. д., ординаты которых есть пределы выносливости для соответствующих циклов напряжений. Точка D, лежащая одновременно и на биссектрисе OD, характеризует предельное напряжение (предел прочности) для постоянной нагрузки у которой 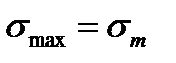 .
.
Так как для пластичных материалов опасным напряжением является также предел текучести 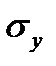 , то на диаграмме наносится горизонтальная линия KL, ордината которой равна
, то на диаграмме наносится горизонтальная линия KL, ордината которой равна 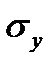 . (для пластичных материалов, диаграмма растяжения которых не имеет площадки текучести, роль
. (для пластичных материалов, диаграмма растяжения которых не имеет площадки текучести, роль 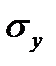 играет условный предел текучести
играет условный предел текучести 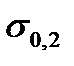 ). Следовательно, диаграмма предельных напряжений окончательно имеет вид CAPKL.
). Следовательно, диаграмма предельных напряжений окончательно имеет вид CAPKL.
Обычно эту диаграмму упрощают, заменяя ее двумя прямыми СМ и ML, причем прямую СМ проводят через точку С (соответствующую симметричному циклу) и точку Р (соответствующую пульсирующему циклу).
Указанный способ схематизации диаграммы предельных напряжений предложен С.В. Серенсеном и Р.С. Кинасошвили.
В этом случае в пределах прямой СМ предельное напряжение цикла (предел выносливости) выражается уравнением
 (11.6)
(11.6)
 или
или
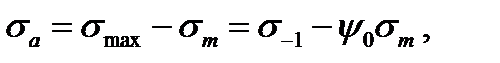 (11.7)
(11.7)
где
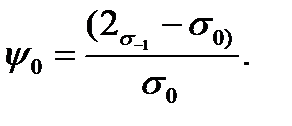 (11.8)
(11.8)
Коэффициент 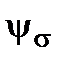 - называется коэффициентом чувствительности материала к асимметрии цикла. Значения
- называется коэффициентом чувствительности материала к асимметрии цикла. Значения 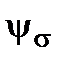 и, аналогично, коэффициент для кручения
и, аналогично, коэффициент для кручения  приведены в табл. 11.1.
приведены в табл. 11.1.
Для построения диаграммы предельных амплитуд цикла по вертикальной оси откладывают амплитуду напряжений цикла, по горизонтальной оси - среднее напряжение цикла 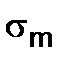 , (рис. 11.7).
, (рис. 11.7).
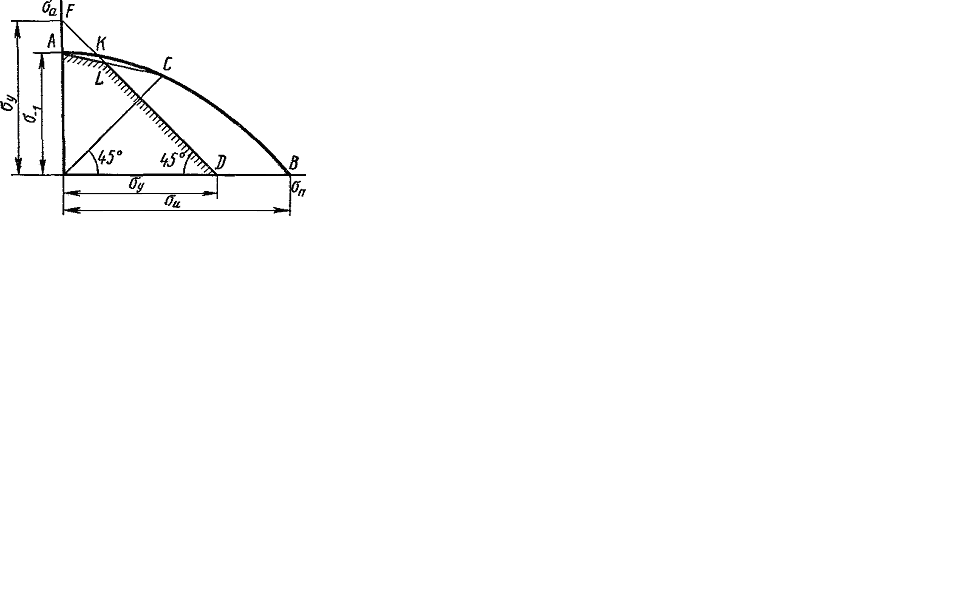
Рис. 11.7.
Точка A диаграммы соответствует пределу выносливости при симметричном цикле, так как при таком цикле 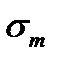 = 0.
= 0.
Точка В соответствует пределу прочности при постоянном напряжении, так как при этом 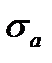 = 0.
= 0.
Точка С соответствует пределу выносливости при пульсационном цикле, так как при этом  .
.
Другие точки диаграммы соответствуют пределам выносливости для циклов с различным соотношением 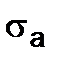 и
и  .
.
Для пластичных материалов предельное напряжение не должно превосходить предела, текучести: 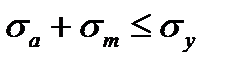 .
.
Поэтому на диаграмму предельных напряжений наносим прямую DE, построенную по уравнению  .
.
Окончательная диаграмма предельных напряжений имеет вид AKD.
На практике обычно пользуются приближенной диаграммой 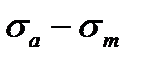 , построенной по трем точкам А, С и Д и состоящей из двух прямолинейных участков AL и LD (способ Серенсена- Кинасошвили). Точка L получается в результате пересечения прямых DE и AC.
, построенной по трем точкам А, С и Д и состоящей из двух прямолинейных участков AL и LD (способ Серенсена- Кинасошвили). Точка L получается в результате пересечения прямых DE и AC.
Расчеты по диаграммам предельных напряжений и предельных амплитуд цикла при одинаковых способах апроксимирования приводят к одним и тем же результатам.
Таблица 11.1.
| Коэффициенты | 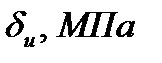
| ||||
| 320-420 | 400-500 | 600-750 | 700-1050 | 1050-1250 | |
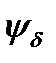 (изгиб, растяжение, сжатие) (изгиб, растяжение, сжатие)
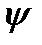 (кручения) (кручения)
| 0,05 | 0,10 0,05 | 0,20 0,10 |
Дата добавления: 2020-10-25; просмотров: 744;











