Минимизация простоя ресурсов при ограничении на время их использования

Собственники ресурсов, с одной стороны, ограничивают время занятия слотов, чтобы сбалансировать доли потоков заданий пользователей и своих (локальных) заданий. С другой стороны, естественным стремлением собственников является минимизация простоя ресурсов. Положим, задано ограничение на время занятия слотов 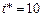. Задача сводится к отысканию комбинаций слотов, обеспечивающих ограничение .

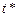Формально эту задачу можно записать в виде

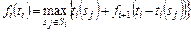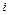, =1, 2, 3, 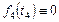. (3.3.13)

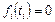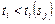Считаем, что при . В результате решения задачи (3.3.13) получаем комбинации слотов, каждая из которых является оптимальной и обеспечивает максимум 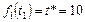и, следовательно, отсутствие простоя ресурсов: (1, 2, 3), (2, 1, 3), (2, 2, 2) и (3, 1, 2).

Заметим, что лишь для комбинаций (2, 2, 2) и (3, 1, 2) цена составляет 20 единиц и является максимальной.

Задача выбора эффективной комбинации слотов

Постановка задачи

Сам характер организации распределенных сред с неотчуждаемыми ресурсами требует многокритериальных моделей планирования заданий.

Пусть 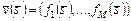– вектор частных критериев 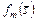, , 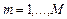например 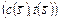. Вектор 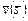формирует бинарное отношение 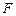сравнительной эффективности комбинаций слотов множества 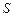, такое что

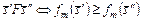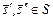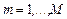, , . (3.4.1)

Положим, имеет место (3.4.1) и при этом 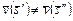. Тогда 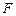- отношение Парето.

Будем применять понятие модели выбора 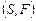и говорить об 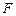-оптимальной стратегии планирования пакета заданий. Стратегия понимается как множество оптимальных по бинарному отношению 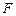комбинаций слотов в модели выбора 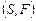. Если, в частности, 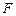- отношение Парето, то речь идет о Парето-оптимальной стратегии. Каждый из критериев 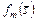формирует частное бинарное отношение

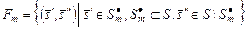. (3.4.2)

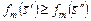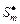При этом в (3.4.2) , а – подмножество комбинаций слотов, одновременно обладающее свойством внешней устойчивости

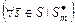
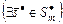
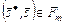(3.4.3)

и внутренней устойчивости

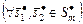
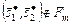(3.4.4)

в модели выбора .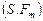

Подмножество 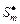множества 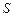комбинаций слотов, определяемое в соответствии с (3.4.2) – (3.4.4), будем называть стратегией, условно оптимальной по частному критерию .

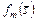Формальная постановка задачи выбора эффективной комбинации слотов при заданном ограничении (3.2.5) заключается в построении 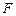-оптимальной стратегии, где 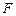формируется вектором 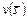критериев, таким что имеет место (3.4.1), и отборе наилучшего компромиссного решения 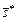путем нахождения экстремума (например, минимума) функции полезности вида

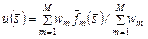, (3.4.5)

где 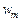– вес частного критерия 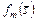, а 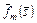– его нормированное значение.

В (3.4.5) нормированное значение любого из критериев определяется согласно соотношению

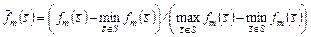. (3.4.6)

Необходимость введения функции полезности (3.4.5) с учетом (3.4.6) обусловлена тем, что из 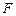-оптимальной стратегии должна быть отобрана одна допустимая комбинация 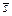подходящих слотов, которая оформляется соответствующими ресурсными запросами, поступающими в виде команд в локальные системы управления ресурсами (пакетной обработки заданий) или планировщики.