Максимизация доходов собственников ресурсов при заданном ограничении на суммарное время использования слотов

Пусть необходимо выбрать комбинацию слотов для выполнения пакета из трех заданий (см. табл. 3.1) такую, чтобы обеспечить максимум суммарной стоимости (3.2.1) использования ресурсов. Задано ограничение на суммарное время занятия слотов заданиями в соответствии с (3.2.6), (3.2.7):

.

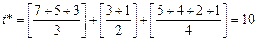Решение задачи проведем поэтапно, используя схему обратной прогонки (3.3.1), (3.3.2) и ассоциируя 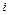-й этап с получением максимального дохода собственников ресурсов на этапах 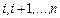. Согласно (3.3.1)

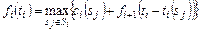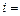, 1, 2, 3, 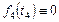. (3.3.7)

В (3.3.7) максимум отыскивается по допустимым для 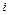-го задания наборам 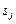слотов.

В соответствии со схемой обратной прогонки определим состояние 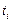следующим образом: 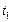– суммарное время занятия слотов заданиями 1, 2 и 3; 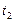– суммарное время занятия слотов заданиями 2 и 3; 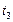– время занятия слотов заданием 3. Таким образом, 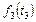– максимальный доход от использования слотов заданием 3 (этап 3) при 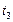; 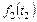– максимальный доход от использования слотов заданиями 2 и 3 (на этапах 2 и 3) при 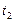; 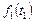– максимум дохода, получаемого собственниками ресурсов от выполнения заданий 1, 2 и 3 (на этапах 1, 2 и 3) при 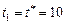. Полагаем, что 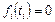при .

Пр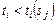оведем поэтапные расчеты, связанные с получением максимума доходов собственников ресурсов:

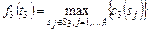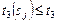, ; (3.3.8)

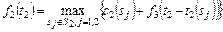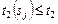, , (3.3.9)

где значения 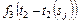определяются из (3.3.8);

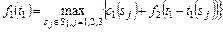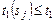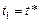, , . (3.3.10)

В (3.3.10) значения 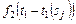вычисляются по (3.3.9). В (3.3.8)-(3.3.10) 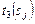, 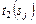и 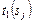берутся из табл. 3.1. Результаты расчетов по (3.3.8) и (3.3.9) приведены в табл. 3.2 и 3.3 соответственно.

Максимум доходов 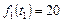собственников ресурсов обеспечивается при использовании заданием 1 наборов 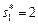или .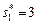

Получение оптимальных наборов слотов для заданий 2 и 3 и, следовательно, комбинации слотов для всего пакета заданий, можно представить в виде следующей схемы:

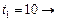
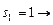
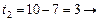
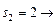
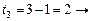
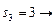(1, 2, 3),

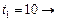
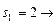
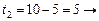
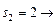
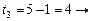
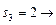(2, 2, 2),

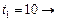
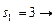
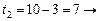
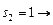
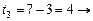
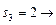(3, 1, 2).

Таблица 3.2

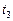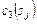
Время занятия слотов заданием 3		Оптимальное решение для заданного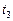
	-	-	-	-		-
	-	-	-
	-	-
	-	-
	-
…	…	…	…	…	…	…

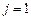
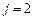
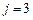
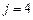
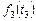
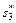
Положим 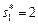. Тогда на выполнение заданий 2, 3 требуется выделить время 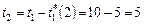, поскольку 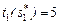(табл. 3.1). При 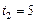максимум 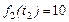обеспечивается набором 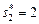слотов согласно (3.3.9). В свою очередь, на выполнение задания 3 остается время, равное 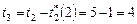, так как 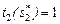(табл. 3.1). Значит, в соответствии с (3.3.8) получаем, что 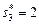. Оптимальной является комбинация слотов (2, 2, 2). Максимум доходов собственников ресурсов достигается также при выделении комбинации (3, 1, 2).

Заметим, что при фиксированном бюджете 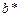виртуальной организации рассмотренная задача аналогична задаче минимизации потерь доходов собственников ресурсов.

Таблица 3.3

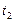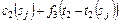
Суммарное время занятия слотов заданиями 2 и 3		Оптимальное решение для заданного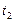
	-	-		-
	-	-		-
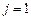
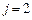
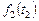
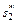
	-	2+4=6
	-	2+6=8
	3+4=7	2+6=8
	3+6=9	2+8=10
	3+6=9	2+8=10
	3+8=11	2+8=10
…	…	…	…	…
	3+8=11	2+8=10