Схема выбора эффективной комбинации слотов

Для отыскания 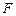-оптимальной стратегии выполнения системы заданий необходимо формирование стратегий, которые являются условно оптимальными по частным критериям и удовлетворяют (3.4.2)-(3.4.4).

Пусть 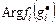, , 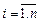представляет собой множество значений функции затрат 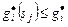, при которых достигается экстремум 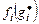для заданного 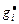в схемах обратной (3.3.1), (3.3.2) и прямой (3.3.3), (3.3.4) прогонки.

Тогда для (3.3.1), (3.3.2) справедливо

, ,

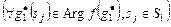
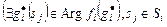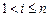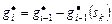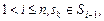
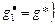
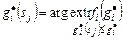, . (3.4.7)

Для схемы (3.3.3), (3.3.4)

, ,

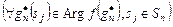
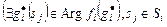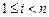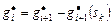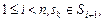
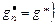
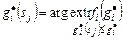, . (3.4.8)

Условно оптимальный набор слотов для выполнения 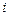-го задания будем обозначать через .

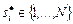Условно оптимальная комбинация слотов 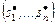определяется из уравнения

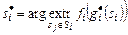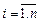, , (3.4.9)

где значения 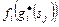получаются из (3.4.7), (3.4.8).

Так, в множество условно оптимальных (при заданном 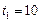) входит комбинация слотов (1, 2, 3), полученная при решении задачи в подразделе 3.3.3, когда 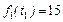. Все три комбинации слотов, упомянутые в подразделе 3.3.3, условно оптимальны по критерию 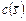в соответствии с (3.4.9), поскольку они образуют множество альтернатив, являющееся внутренне и внешне устойчивым в соответствующей модели выбора, где бинарное отношение вида (3.4.2) порождается критерием 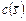. Условно оптимальными являются комбинации (1, 2, 4) и (2, 2, 4), полученные при решении соответствующей задачи в подразделе 3.4. Они дают суммарное время выполнения пакета заданий, соответственно равное 9 и 7 единицам времени, а затраты составляют 13 и 16 единиц.

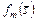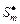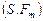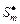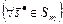
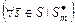
При применении схем (3.3.1), (3.3.2) и (3.3.3), (3.3.4) для каждого из критериев эффективности верны соотношения (3.4.2)-(3.4.4). Действительно, условно оптимальные комбинации слотов согласно (3.4.9) образуют внутренне устойчивое множество комбинаций в модели выбора . Внешняя устойчивость следует из того, что 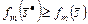. Наборы вида (3.4.9) позволяют построить условно оптимальные стратегии и в конечном итоге найти 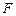-оптимальную стратегию и наиболее эффективную комбинацию слотов для выполнения пакета заданий.

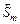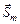Обозначим через и стратегии, условно оптимальные по критерию 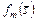, полученные соответственно по схемам обратной (3.3.1), (3.3.2) и прямой (3.3.3), (3.3.4) прогонки. Заметим, что в общем случае 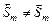. Пусть 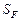является 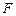-оптимальной стратегией в модели выбора 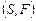, где бинарное отношение 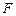удовлетворяет (3.4.1). Положим, , где 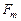определяется согласно (3.4.2). Тогда 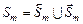является стратегией, условно оптимальной по критерию 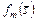, поскольку имеет место (3.4.3), (3.4.4).

Предположим, что

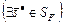
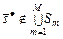. (3.4.10)

Внешняя устойчивость 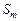в модели выбора 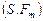исключает существование такой комбинации слотов 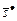и делает невозможным (3.4.10).

Далее, в силу внутренней устойчивости 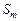в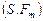

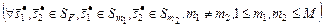
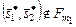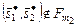, . (3.4.11)

В общем случае 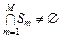. Пусть 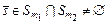, 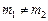. Тогда

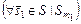
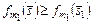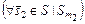
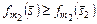, . (3.4.12)

Из-за невозможности выполнения (3.4.10) и справедливости (3.4.11), (3.4.12) следует, что

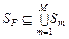. (3.4.13)

Таким образом, применение схем (3.3.1), (3.3.2) и (3.3.3), (3.3.4) позволяет сформировать частные стратегии 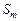, условно оптимальные по каждому из критериев эффективности 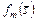, а 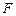-оптимальная стратегия согласно (3.4.13) отыскивается на объединении частных стратегий.

В частности, если 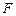является отношением Парето, то речь идет о Парето-оптимальной стратегии. При этом отношение Парето представляет собой асимметричную часть отношения 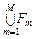, поскольку справедливо (3.4.1) и при этом .

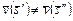3.4.3. Формирование 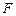-оптимальной стратегии планирования при заданных ограничениях

Положим, необходимо сформировать 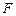-оптимальную стратегию выполнения пакета заданий, характеристики которых приведены в табл. 3.1. В соответствии с (3.4.13) 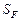строится на объединении стратегий, сформированных с применением частных критериев (подраздел 3.4.2). Пусть 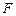в (3.4.1) формируется критериями (3.2.1), (3.2.2).

В табл. 3.4 приведены стратегии, условно оптимальные по критериям стоимости 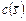и времени 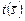выполнения пакета заданий. Они включают 13 комбинаций слотов (планов), которые сформированы в ходе решения модельных задач, рассмотренных в подразделах 3.3.3 –3.3.6 методом обратной прогонки по (3.3.1), (3.3.2). Варианты 14 - 25 получены методом прямой прогонки в соответствии с (3.3.3), (3.3.4). Планы 1 – 3; 7 – 9; 14 – 16; 20 – 22 являются условно оптимальными по 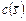, а планы 4 – 6; 10 – 13; 17 – 19; 23 – 25 – по .

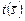Некоторые из планов, полученных при формировании стратегий с применением различных критериев и схем прогонки, совпадают. В табл. 3.4 это, например, планы 4, 7; 5, 8; 6, 9; 1, 10; 2, 12; 3, 13; 11, 15; 14, 17 и т.д. Оставим лишь первый план из пары совпадающих и сведем их в табл. 3.5.

Таблица 3.4

План	Комбинация	Критерий
	слотов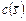
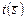
	(1,2,3)
	(2,2,2)
	(3,1,2)
	(1,2,4)
	(2,2,4)
	(3,2,4)
	(1,2,4)
	(2,2,4)
	(3,2,4)
	(1,2,3)
	(2,1,3)
	(2,2,2)
	(3,1,2)
	(3,2,1)
	(2,1,3)
	(2,1,4)
	(3,2,1)
	(3,2,2)
	(3,2,3)
	(3,2,1)
	(3,2,2)
	(1,2,3)
	(3,2,1)
	(2,1,4)
	(1,2,4)

В ней представлены относительные (нормированные) в соответствии с (3.4.6) значения критериев 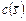, 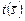для планов, обозначенных как .

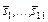В пространстве критериев 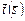и 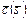, имеющих одинаковую важность, альтернативы 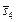и 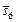доминируют над всеми остальными и образуют подмножество Парето (рис. 3.2).

Таблица 3.5

План	Комбинация слотов	Нормированный критерий	Функция полезности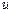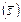
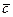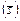
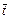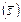
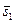
	(1,2,3)	0,29		0,65
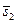
	(2,2,2)
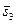
	(3,1,2)
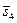
	(1,2,4)		0,80	0,40
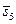
	(2,2,4)	0,43	0,40	0,42
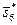
	(3,2,4)	0,29		0,15*
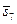
	(2,1,3)	0,86		0,93
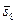
	(3,2,1)	0,43	0,80	0,62
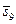
	(2,1,4)	0,57	0,80	0,69
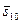
	(3,2,2)	0,86	0,60	0,73
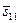
	(3,2,3)	0,57	0,20	0,39

Конкретная комбинация слотов должна выбираться из стратегии и оформляться соответствующими ресурсными запросами, поступающими в локальные системы пакетной обработки. При этом эффективность той или иной комбинации слотов можно оценить с помощью скалярной функции полезности (3.4.5).

Положим, веса нормированных в соответствии с (3.4.6) критериев 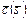, 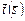равны. Тогда наилучшим компромиссным решением является план 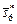с минимальным значением 0,15 функции полезности 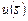. Именно этот план и должен быть оформлен ресурсными запросами к локальным вычислительным узлам в виде резервирования соответствующих слотов.

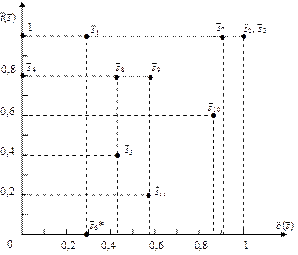
Рис. 3.2. Пример стратегии планирования в пространстве

двух критериев

Выводы

В данном разделе рассмотрено решение задач планирования пакетов независимых заданий в распределенных средах с неотчуждаемыми ресурсами на основе методов динамического программирования и циклической схемы. Стратегия планирования строится с применением вектора критериев, формализующих экономическую политику предоставления и потребления ресурсов в виртуальной организации, объединяющей пользователей, собственников и администраторов.

Однако этой схеме присущи следующие ограничения. Отсутствует возможность влиять на ход выполнения отдельного пользовательского задания: поиск отдельных альтернатив осуществляется по принципу «первая подходящая», а выбор их оптимальной комбинации отражает интересы всей виртуальной организации. Таким образом, не учитываются предпочтения отдельных пользователей, что не позволяет говорить о справедливом разделении ресурсов. Преодолеть эти ограничения позволяет теоретико-игровой подход к планированию, основы которого излагаются в следующем разделе.

4. МНОГОАГЕНТНОЕ ВЗАИМОДЕЙСТВИЕ и элементы теории игр

4.1. Введение и основные понятия теории игр

Введение

При планировании распределенных вычислений с использованием экономических принципов необходимо учитывать интересы и особенности поведения многочисленных участников вычислений: пользователей, запускающих задания, владельцев ресурсов и администраторов виртуальной организации. Как правило, интересы участников вступают в конфликт, так как каждый из них, прежде всего, заинтересован в максимизации личной выгоды. Именно поэтому при проектировании механизма планирования необходимо понимать, как будут вести себя основные участники: какие цели они преследуют, какие имеют способы их достижения, каким образом происходит ценообразование и т.п. Кроме того, одним из образующих качеств виртуальной организации, кроме эффективности планирования, является наличие прозрачных и справедливых правил разделения и использования доступных ресурсов и полученной прибыли.

Для того чтобы приблизиться к пониманию и решению этих проблем мы предлагаем использовать теоретико-игровой подход и далее представим некоторые элементы теории игр, наиболее существенные для анализа и решения поставленных задач. Так, в разделе 4.2 рассматривается проблема выбора стратегий поведения рациональными соперниками, раздел 4.3 содержит и примера механизма, обладающего необходимыми и предсказуемыми экономическими свойствами, а в разделе 4.4 на примере сетевых моделей продемонстрирован итеративный алгоритм распределения сетевых ресурсов.