Постановка задачи выбора оптимальной комбинации слотов

Планирование выполнения пакета независимых заданий осуществляется циклично. В цикле планирования задания упорядочиваются в соответствии с приоритетами, например, в порядке поступления в очередь метапланировщика или иерархической структуры промежуточных серверов. Задания могут группироваться в пакеты по схожести ресурсных требований к вычислительным узлам (архитектуре, составу), в соответствии с политикой администрирования, реализуемой в том или ином домене узлов.

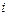Пусть – множество наборов слотов, подходящих для выполнения -го задания пакета, 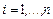. Набор слотов 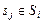является подходящим для 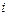-го задания, если он удовлетворяет требованиям ресурсного запроса, цене 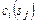и времени 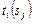, 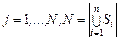. Ресурсный запрос содержит тип, количество и характеристики необходимых узлов (тактовую частоту процессора, емкость оперативной памяти, дисковое пространство, операционную систему и т.д.). При этом 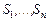не обязательно не пересекаются. К началу каждого цикла планирования локальные расписания обновляются и известны. При этом требуется решение двух задач. Во-первых, нужно отобрать набор подходящих слотов для каждого задания 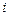пакета. Во-вторых, необходимо найти комбинацию слотов, оптимальную с позиции прохождения всего пакета заданий в текущем цикле планирования. Комбинация представляет собой 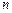-элементную последовательность 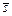не обязательно различных наборов слотов. Любое из заданий может использовать один и только один набор слотов. В то же время некоторые из наборов могут разделяться по времени или ресурсу несколькими заданиями одного и того же пакета. Обозначим через 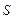множество комбинаций слотов для пакета заданий. Если для какого-либо из заданий подходящего набора слотов не существует, то его планирование переносится в следующий цикл и задание занимает место в очереди цикла планирования в соответствии с некоторым приоритетом. После просмотра слотов для всех 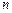заданий пакета отыскиваются альтернативные наборы слотов, поскольку при отборе слотов для 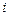-го задания не весь исходный список может быть просмотрен. Эта процедура итеративно реализуется для всех заданий, планирование которых не перенесено в следующий цикл.

Рассматриваются два типа критериев, формализующих экономическую политику предоставления и потребления ресурсов в виртуальной организации, - стоимостные и временны́е показатели прохождения пакета заданий на допустимой комбинации 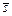подходящих наборов слотов. Политика реализуется метапланировщиком, оптимизирующим план выполнения потоков или пакетов, а не отдельных заданий. При этом в качестве критериев оптимизации используются, как правило, обобщенные (аддитивные) показатели. Приведем их примеры.

Независимые пользователи конкурируют между собой за тот или иной ресурс. С одной стороны, пользователь, увеличивая плату за выполнение задания, вправе рассчитывать на приближение момента его запуска на более производительном ресурсе. С другой стороны, он стремится минимизировать свои затраты.

Политика администрирования, принятая в виртуальной организации, направлена на такое распределение ресурсов, которое является оптимальным с позиций суммарной стоимости выполнения всего пакета заданий:

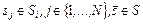, . (3.2.1)

Примером временно́го показателя, который отражает интересы пользователей и политику администрирования, является суммарное время прохождения пакета:

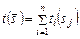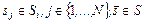, . (3.2.2)

Пусть – функция, определяющая эффективность выполнения 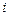-го задания на наборе 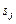слотов при допустимых затратах 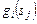. В частности, 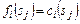– стоимость использования набора 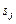в течение времени 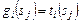либо 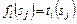– время выполнения 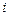-го задания на наборе 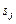слотов стоимостью 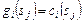. Цена набора – сумма цен составляющих его слотов.

Полагаем, что критерий эффективности прохождения пакета заданий представляет собой сепарабельную функцию

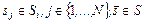, , (3.2.3)

в частности (3.2.1) или (3.2.2).

Задается ограничение на суммарные затраты для выполнения всего пакета заданий. В частности, для того чтобы не допустить монополизации использования какого-либо ресурса, вводится ограничение 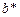на бюджет виртуальной организации – максимальное значение 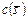в (3.2.1) для текущего цикла планирования. Доходы собственников тем больше, чем большее время их ресурсы задействованы в вычислениях внешними заданиями. Однако требование сбалансированности долей глобальных и локальных потоков заданий заставляет собственников вводить ограничение 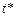на суммарное время занятия слотов (3.2.2).

Ограничение формируется динамично к началу текущего цикла планирования таким образом, что

, (3.2.4)

где 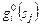– функция уровня ресурсных затрат, учитывающая характеристики подходящих наборов слотов для каждого задания пакета (подчеркнем, что множество доступных слотов в каждом цикле планирования известно).

Формальная постановка задачи выбора оптимальной комбинации слотов 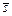заключается в отыскании экстремума (3.2.3) при ограничении

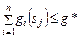, (3.2.5)

где определяется в соответствии с (3.2.4).

Еще раз отметим, что ограничение (3.2.5) формируется для каждого пакета в текущем цикле планирования. Рассмотрим пример ограничения (3.2.4), фигурирующего в правой части неравенства (3.2.5).

Функция уровня временны́х затрат может иметь следующий вид:

, (3.2.6)

где – число подходящих (альтернативных) наборов слотов для 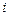-го задания; 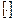– ближайшее не большее целое число.

Ограничение (3.2.4) с учетом (3.2.6) задается следующим образом:

. (3.2.7)

В (3.2.7) 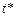– сумма усредненных значений длительности слотов по всем альтернативным наборам в пакете.

В задачах однокритериальной оптимизации каждая из сторон, представленная в виртуальной организации, – пользователь, собственник, администратор – заинтересована в минимизации или максимизации критериев типа (3.2.1), (3.2.2) при заданных ограничениях путем выбора оптимальной комбинации 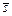слотов. Например, пользователи стремятся минимизировать стоимость 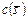(3.2.1) при ограничении на суммарное время 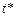занятия слотов (3.2.7) либо минимизировать время (3.2.2) прохождения пакета заданий при фиксированном бюджете 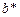виртуальной организации. С позиций собственников ресурсов целесообразно минимизировать потери доходов (максимизировать 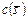) или простой ресурсов (максимизировать ) при ограничении на время использования слотов внешними заданиями. Конкретные задачи поиска оптимальной комбинации слотов рассматриваются в разделе 3.3 настоящего пособия.