Решение задачи и примеры выбора оптимальной комбинации слотов

В данном разделе рассматривается отыскание экстремума (3.2.3) при ограничении (3.2.5). Приводится ряд примеров, имеющих важное практическое значение.

Схема выбора

Пакет состоит из 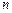независимых заданий, что допускает естественную декомпозицию решения задачи (3.2.3)-(3.2.5) на 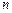этапов с использованием методов динамического программирования, основанных на рекуррентных соотношениях.

Для этого необходимо ввести понятие состояния системы (пакета заданий). Его будем представлять уровнем 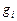допустимых суммарных затрат на выполнение части заданий пакета, включая 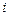-е задание, например заданий 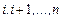либо заданий .

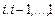В частности, в одном случае 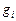может представлять собой суммарное время 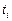занятия слотов заданиями 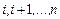либо заданиями 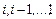. В другом случае, 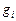– суммарная стоимость 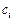использования слотов заданиями 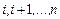или .

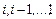Подчеркнем, что 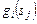в отличие от 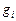обозначает затраты на выполнение 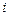-го задания на наборе 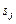слотов - цену 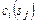или время 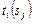(раздел 3.2).

Тогда рекуррентные соотношения для отыскания экстремума (3.2.3) при ограничении (3.2.5) и использовании набора слотов 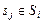, 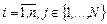по схеме обратной прогонки имеют следующий вид:

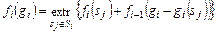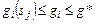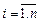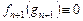, , , ; (3.3.1)

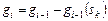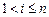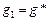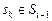, , , , (3.3.2)

где 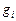– суммарные затраты при использовании наборов слотов заданиями 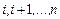пакета.

Соответствующие уравнения для схемы прямой прогонки:

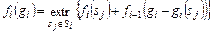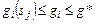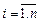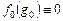, , , ; (3.3.3)

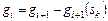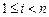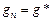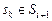, , , , (3.3.4)

где 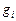– суммарные затраты на выполнение заданий 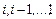пакета.

Оптимальные затраты в схемах (3.3.1), (3.3.2) и (3.3.3), (3.3.4) определяются из уравнения

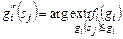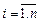, . (3.3.5)

Оптимальный набор слотов для выполнения 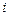-го задания будем обозначать через .

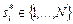В обеих схемах (3.3.1), (3.3.2) и (3.3.3), (3.3.4) он задается соотношением

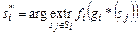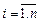, . (3.3.6)

На основе функциональных уравнений (3.3.1)-(3.3.6) отыскивается решение задачи (2.2.3) при ограничении (2.2.5), позволяющее получить оптимальную комбинацию слотов 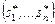для пакета заданий.