Понятие функции алгебры логики

Функция, однозначно определяющая соответствие каждой из всех возможных совокупностей значений аргументов нулю или единице, называется функцией алгебры логики (ФАЛ).

Логические переменные – как функция, так и аргументы, могут принимать только два значения. Обычно их обозначают символами 0 и 1.

Для технической реализации ФАЛ используют электрические схемы, называемые логическими элементами. Логический элемент (ЛЭ) выполняет логические операции над одной или более логическими переменными. При этом переменная-функция соответствует выходу ЛЭ, а переменные-аргументы – разрядам двоичных наборов, поступающим на соответствующие входы ЛЭ.

Закон функционирования ЛЭ представляют в виде таблицы истинности (рис. 1). В строках первого раздела этой таблицы по порядку записываются десятичные номера входных двоичных наборов. В строках второго раздела записываются собственно входные наборы, представляющие собой n-разрядное двоичное отображение соответствующего десятичного номера. В строках третьего раздела записываются соответствующие входным наборам значения функции.

В общем случае ФАЛ строятся на основе элементарных ФАЛ. Элементарной называется ФАЛ одного или двух аргументов, в логическом выражении которой содержится не более одной логической операции.

К элементарным ФАЛ одного аргумента относятся:

1. Константа нуля. Реализуется генератором нуля, который на схемах обозначается соединением соответствующего входа ЛЭ с «землей» (общим проводом источника питания).

2. Константа единицы. Реализуется генератором единицы, который на схемах обозначается соединением соответствующего входа ЛЭ с полюсом источника питания.

3. Повторение. Реализуется логическим элементом повторителем. Его условное графическое обозначение и таблица истинности показаны на рис. 2. Записывается ФАЛ как у = х.

4. Инверсия или логическое отрицание. Реализуется логическим элементом НЕ (инвертором). Его условное графическое обозначение и 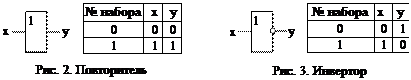таблица истинности показаны на рис. 3. Записывается ФАЛ как у = .

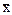Основными из элементарных ФАЛ двух аргументов являются:

1. Дизъюнкция (логическое сложение). Реализуется логическим элементом ИЛИ. Его условное графическое обозначение и таблица истинности показаны на рис. 4. Записывается ФАЛ как у = aÚb.

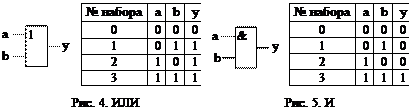2. Конъюнкция (логическое умножение). Реализуется логическим элементом И. Его условное графическое обозначение и таблица истинности показаны на рис. 5. Записывается ФАЛ как у = aÙb.

3. Стрелка Пирса. Реализуется логическим элементом ИЛИ-НЕ. Его условное графическое обозначение и таблица истинности показаны на рис. 6. Записывается ФАЛ как 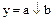и может быть представлена в сложной форме: .

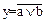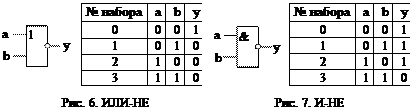4. Штрих Шеффера. Реализуется логическим элементом И-НЕ. Его условное графическое обозначение и таблица истинности показаны на рис. 7. Записывается ФАЛ как y = a | b и может быть представлена в сложной форме: .

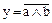5. Исключающее ИЛИ (сложение по модулю два). Реализуется сумматором по модулю два. Его условное графическое обозначение и таблица истинности показаны на рис. 8. Записывается ФАЛ как у = 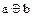и может быть представлена в сложной форме: у = 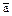Ùb Ú аÙ .

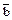6. Эквивалентность. Реализуется одноименным ЛЭ. Его условное графическое обозначение и таблица истинности показаны на рис. 9. Записывается ФАЛ как y = a∾b и может быть представлена в сложной форме: у = 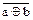= 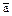Ù 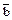Ú аÙb.

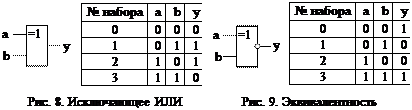Функции дизъюнкция и штрих Шеффера с одной стороны, конъюнкция и стрелка Пирса с другой, являются частными случаями функций конституанты (постоянной) нуля и единицы, соответственно.

Функция конституанты единицы (нуля) от n аргументов обращается в единицу (ноль) лишь на каком-либо одном наборе аргументов и обращается в ноль (единицу) на остальных наборах.

Все рассмотренные функции могут быть расширены на произвольное число аргументов.