Вывод минимальной ФАЛ
Структурная схема логического устройства может быть построена непосредственно по канонической форме (СДНФ или СКНФ) реализуемой функции. Получающиеся схемы обеспечивают правильное функционирование устройства, но оказываются неоправданно сложными, требуют использования большого числа логических элементов и, следовательно, имеют низкие экономичность и надежность.
Во многих случаях удается так упростить логическое выражение, не нарушая функции, что соответствующая структурная схема оказывается существенно более простой. Такое упрощение функций называется минимизацией.
Минимизировать можно с использованием законов алгебры логики (законы склеивания и поглощения) и графическими методами (с использованием карт Карно и диаграмм Вейча). При минимизации получаются минимальная дизъюнктивная нормальная форма (МДНФ) и минимальная конъюнктивная нормальная форма (МКНФ).
Метод минимизации функции с помощью карт Карно (диаграмм Вейча) обеспечивает простоту получения результата. Он используется при минимизации относительно несложных функций (с числом аргументов не более пяти). Карта Карно (диаграмма Вейча) представляет собой определенную форму таблицы истинности. На рисунке приведены карты Карно и диаграммы Вейча для функций двух (а), трех (б), четырех (в) аргументов. Каждая клетка карты соответствует определенному набору аргументов. Этот набор аргументов определяется присвоением значения лог.1 буквам, на пересечении строк и столбцов которых расположена клетка.
Карты Карно
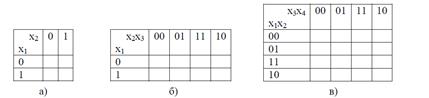
Диаграммы Вейча
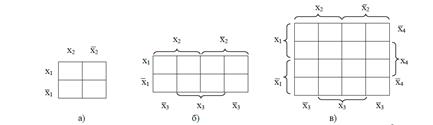
Число клеток диаграммы равно числу всех возможных наборов значений аргументов. В каждую из клеток диаграммы записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пример карты Карно и диаграмма Вейча для функции, заданной в таблице, представлена на рисунке.
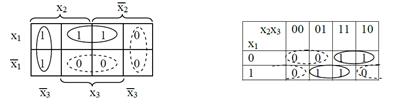
Правила получения МДНФ (МКНФ):
· все клетки, содержащие единицы (нули), объединяются в замкнутые области.
· каждая область должна быть прямоугольной с числом клеток 1, 2, 4, 8.
· области могут пересекаться и одни и те же клетки могут входить в разные области.
· при охвате клеток областями следует стремиться к минимальному числу областей и максимальному числу клеток в каждой области.
· МДНФ (МКНФ) будет содержать столько конъюнкций (дизъюнкций), сколько получилось областей; в каждую конъюнкцию (дизъюнкцию) будут входить аргументы, одинаковые для всех клеток области (с инверсией или без нее).
· при записи МКНФ аргументы карты Карно (диаграммы Вейча) необходимо проинвертировать.
МДНФ для рассматриваемой функции:
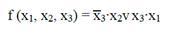
МКНФ для рассматриваемой функции:
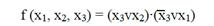
По полученным МДНФ и МКНФ строится схема КЦУ в базисе И, ИЛИ, НЕ. Перед построе-нием надо определить, какие логические элементы и сколько их потребуется для построения схемы.
Для построения схемы КЦУ по МДНФ потребуется один элемент НЕ, два элемента И, один элемент ИЛИ. Схема имеет вид:
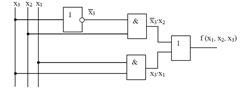
Для построения схемы КЦУ по МКНФ потребуется один элемент НЕ, два элемента ИЛИ, один элемент И. Схема имеет вид:
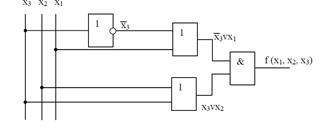
Для того чтобы построить схему в базисах И-НЕ (ИЛИ-НЕ) необходимо МДНФ (МКНФ) функции перевести в соответствующий базис, применив закон двойного отрицания и закон де Моргана.
Преобразование МДНФ в базис И-НЕ:
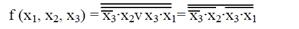
Схема, построенная по этому выражению, имеет вид:
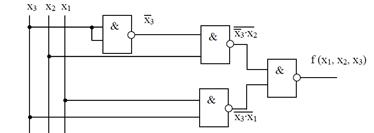
Преобразование МКНФ в базис ИЛИ-НЕ:
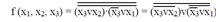
Схема, построенная по этому выражению, имеет вид:
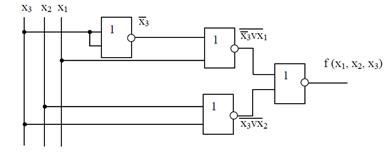
Минимизация методом Квайна заключается в следующем.
1. Члены исходной ФАЛ, где учтены и безразличные входные наборы, отличающиеся только в одной переменной, группируются в пары.
Две ФАЛ отличаются в одной переменной, если эта переменная в одну из них входит с инверсией, а в другую без инверсии. Других различий нет.
При группировке руководствуются следующими правилами:
– пары могут пересекаться, т.е. один и тот же член функции может входить в различные пары;
– при условии участия в процедуре группирования всех членовФАЛ, число пар должно быть минимальным.
2. К сформированным парам в случае СДНФ применяется операция склеивания, а в случае СКНФ – операция поглощения.
3. По результатам преобразования записывается новая ФАЛ, к которой применяются законы и тождества алгебры логики или повторно все пункты минимизации. При этом полезным бывает соотношение 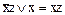 .
.
Дата добавления: 2020-10-25; просмотров: 663;











