Основные законы и тождества алгебры логики

Тождества:

х Ú х = х, х Ú 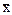= 1, х Ú 1 = 1, х Ú 0 = х,

х Ù х = х, х Ù 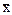= 0, х Ù 1 = х, х Ù 0 = 0,

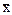х Å х = 0, х Å = 1, х Å 1 = 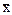, х Å 0 = х.

Законы:

- двойной инверсии – 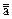= а;

- сочетательный – aÙ(bÙс) = (аÙb)Ùс, аÚ(bÚс) = (аÚb)Úс,

а Å (b Å с) = (а Å b) Å с;

- переместительный – аÙb = bÙа, аÚb = bÚа, а Å b = b Å а;

- распределительный – аÙ(bÚс) = аÙb Ú аÙс,
аÚ(bÙс) = (аÚb)Ù(аÚс),
аÙ(b Å с) = аÙb Å аÙс;

- двойственности (правила де Моргана) –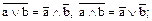

- поглощения – а Ú аÙс = а, aÙ(aÚc) = a;

- склеивания – аÙ 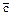Ú aÙc = a, (aÚ 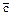)Ù(aÚc) = a.

Все указанные законы и тождества справедливы для любого числа аргументов, причем аргументом может быть как простая переменная, так и функция.

Законы и тождества алгебры логики используются для преобразования ФАЛ в процессе синтеза цифровых устройств. В частности, целью преобразования может быть упрощение ФАЛ:

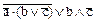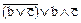у = = аÚ = а Ú 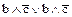= а Ú b Å с.

Кроме того, в тождествах отражены правила замены логических элементов одного типа логическими элементами другого типа.