Фазовое пространство и фазовая плоскость

При составлении уравнений динамики нелинейной системы все звенья, поддающиеся линеаризации в преде­лах малых отклонений координат, описываются линейны­ми уравнениями. Для одного или двух (реже — несколь­ких) нелинейных звеньев этой системы составляются нелинейные уравнения (или используются нелинейные характеристики). В общем случае нелиней­ные дифференциальные уравнения динамики в нормаль­ной форме имеют вид

,

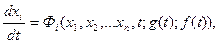
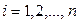где 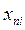—координаты состояния системы, ( ),

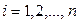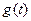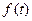, —соответственно задающие и возмущающие воздействия, или в векторной записи

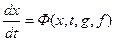
Для рассмотрения переходных процессов, вызванных какими-либо начальными отклонениями координат (при отсутствии внешних воздействий) эти уравнения для систем с постоянными параметрами (т. е. для стационарных систем) принимают вид

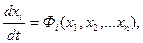
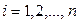, (1.19)

а в векторной форме

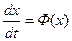
Представим себе n-мерное пространство ко­ординат состояния системы 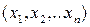(рис. 1.23). Тогда начальное со­стояние системы 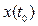изобразится определенной точкой 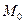с координатами 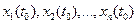,а процесс во времени, т. е. решение уравнений (1.1)

,

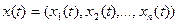может быть изображен в виде некоторой кривой (рис. 1.23). Текущая точка Мна ней, соот­ветствующая состоянию систе­мы в произвольный момент вре­мени t,называется изображаю­щей точкой. Отметим, что зна­чения нелинейных функций 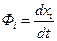стоящих в уравнениях (1.19) справа, определяют в каж­дый момент времени проекции скорости v изображающейточ­ки М на оси координат .

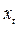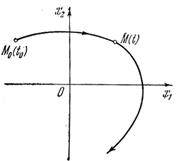
Рис.1.23. Траектория Рис.1.24. Траектория

системы в пространстве системы на пло­скости

Если в многомерном пространстве мы лишь мысленно можем представить себе геометрическую карти­ну, то, например, для системы второго порядка 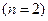можно реально изображать траектории на пло­скости (рис. 1.24).

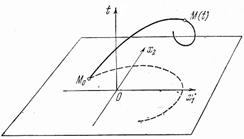
Рис.1.25. Интег­ральная кривая

При этом можно изобразить и интег­ральную кривуюдля данной системы, добавив ось вре­мени t (рис. 1.25).

Уравнения (1.19), при 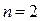, принимают вид

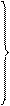
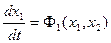
(1.20)

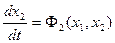
Дифференциальное уравнение фазовой траектории полу­чается путем деления второго уравнения системы(1.20) на первое:

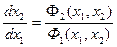(1.21)

Точки равновесного состояниясистемы определяются ну­левыми значениями скорости 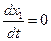, 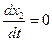; сле­довательно, в этих точках

,

,

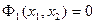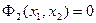что создает неопределенность правой части уравнения (1.21). Поэтому точки равновесного состояния системы яв­ляются так называемыми особыми точкамина фазовой плоскости.

Сопоставим изображение переходного процесса в виде фазовых траекторий на плоскости 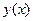с обыч­ным его изображением в виде кривой .

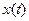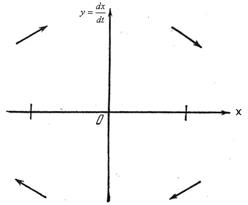
Рис.1.26.Движение по фазовым

тра­екториям

Для удобства положим, что уравнения (1.20) имеют более простой вид:

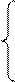
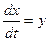
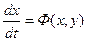
т. е. координата у,откла­дываемая по оси ординат фазовой плоскости, пред­ставляет собой скорость изменения координаты х,откладываемой по оси абсцисс. В этом случае для изображающей точкиспра­ведливо следующее правило для направления движения по фазовым тра­екториям:

а) в верхней полуплоскости (рис. 1.26)— слева направо, т. е. в сторону увеличения х, так как там скорость ;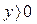

б) в нижней полуплоскости, наоборот,— справа на­лево,

в) ось х пересекается фазовыми траекториями под прямым углом, так как там скорость 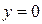, т.е. имеет место максимум или минимум величины х.

Заметим, что это правило недействительно в общем случае уравнения (1.20).

а) б)

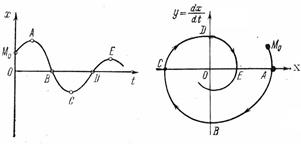
Рис.1.27. Затухающий

колебательный про­цесс

Рассмотрим сначала затухающий колебательный про­цесс 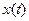(рис. 1.27, а). На фазовую плоскость (рис. 1.27, б),где 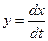,нанесем отмеченные на кри­вой переходного процесса точки А, В, С, ..., в которых х имеет либо максимум, либо нуль, либо минимум. В ре­зультате получим, что затухающий колебательный про­цесс изображается на фазовой плоскости в виде сходя­щейся спиралевидной кривой.

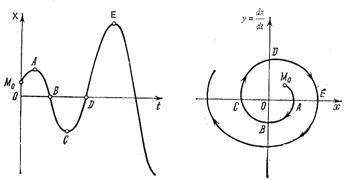
Аналогично расходящийся колебательный процесс(рис. 1.28,а)изобразится на фазовой плоскости в виде расходящейся спиралевиднойкривой(рис. 1.28, б).

а) б)

Рис.1.28. Расходящийся

колебательный процесс

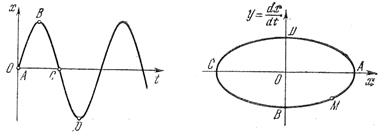
Очевидно, что периодический процесс(рис. 1.29, а)изобразится на фазовой плоскости в виде замкнутой кри­вой(рис. 1.29, б). За один период колебаний изображаю­щая точка Мпробегает весь замкнутый контур, а затем повторяет движение по нему.

а) б)

Рис.1.29. Периодический процесс

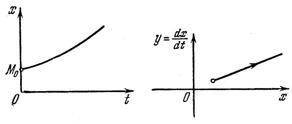
Монотонный затухающий процесс 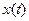(рис. 1.30, а)изобразится на фазовой плоскости в виде кривой, мо­нотонно приближающейся кположению равновесия(рис. 1.30, б), а монотонный расходящийся процесс (рис. 1.31, а) — в виде монотонноудаляющейся кривой (рис. 1.31, б). Удобство представления процесса в виде фазовых траекторий на плоскости состоит в том, что вся совокупность возможных форм переходных процессов в системе при любых начальных условиях представляется в виде единого «фазового портрета». Недостатком же является то, что мы вынуждены при этом ограничиваться рассмот­рением лишь систем второго

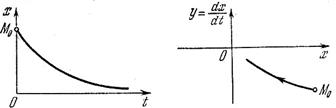
а) б)

Рис.1.30. Монотонный

затухающий процесс

порядка. Для исследования нелинейных систем более высокого порядка будут приме­нены другие методы.

а) б)

Рис.1.31. Монотонный

расходящийся процесс