Преобразования нелинейных статических характеристик
Виды и особенности нелинейных систем
Виды нелинейностей
Нелинейные функции могут быть непрерывными и кусочно-ломаными. Также нелинейные характеристики могут быть однозначные, неоднозначные, симметричные и несимметричные.
Рассмотрим некоторые виды нелинейных характеристик.
Первый вид нелинейных характеристик называется зоной нечувствительности первого рода. Вид такой нелинейной характеристики и схема простейшей механической модели, поясняющей явление зоны нечувствительности(сухое трение), показаны на рис.1.1 и рис.1.2.
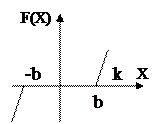
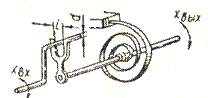
Рис.1.1. Зона Рис.1.2.Механическая
нечувствительности модель зоны
первого рода нечувствительности
первого рода
В рассматриваемом случае входной величиной является угол поворота 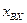 ведущего вала, а выходной — угол поворота
ведущего вала, а выходной — угол поворота 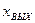 ведомого вала. Пружина всегда стремится вернуть вал в исходное положение, которое удобно выбрать за начало отсчета выходной величины. Ведомый и ведущий валы сцеплены вилкой. Входящий в нее палец имеет диаметр d несколько меньший, чем ширина вилки l; вследствие этого имеется зазор
ведомого вала. Пружина всегда стремится вернуть вал в исходное положение, которое удобно выбрать за начало отсчета выходной величины. Ведомый и ведущий валы сцеплены вилкой. Входящий в нее палец имеет диаметр d несколько меньший, чем ширина вилки l; вследствие этого имеется зазор 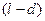 и, пока он не «выбран», ведомый вал не следует за ведущим. За начальное положение ведущего вала удобно принять (при разгруженной пружине) среднее положение его пальца в вилке. Аналитически эта функция записывается как
и, пока он не «выбран», ведомый вал не следует за ведущим. За начальное положение ведущего вала удобно принять (при разгруженной пружине) среднее положение его пальца в вилке. Аналитически эта функция записывается как
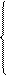
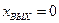 при
при 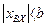
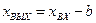 при
при 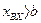
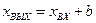 при
при 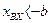
Второй вид нелинейных характеристик называется зоной нечувствительности второго рода (рис.1.3).

| |
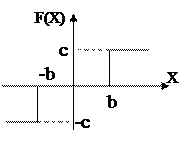
Рис.1.3. Зона нечувствительности Рис.1.4.Механическая
второго рода модель зоны
нечувствительности
второго рода
| |
Примером физической модели (рис.1.4) этого вида нелинейных функций может быть зависимость угловой скорости вращения вала редуктора электрического сервопривода от положения подвижного контакта, включающего электрический ток в обмотки электродвигателя. Эта нелинейная функция также является однозначной. Аналитически рассмотренную функцию можно записать в следующем виде:
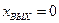 при
при 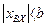
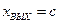 при
при 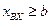
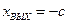 при
при 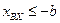
Третьим видом нелинейных характеристик являются нелинейные функции с ограниченной амплитудой выходной величины (рис.1.5).
Если амплитуда выходной величины не выходит за пределы нелинейного участка этой функции, элемент ведет себя как обычное линейное усилительное звено.
| |
| |
| |
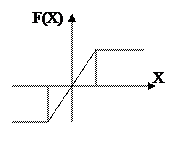
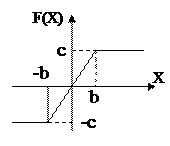
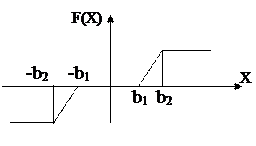
Рис.1.5. Характеристика Рис.1.6. Характеристика с
с ограниченной зоной нечувствительности
амплитудой
| |
В случае возбуждения на входе элемента гармонических колебаний с большой амплитудой выходные колебания перестают быть гармоническими. Искажения эти тем существеннее, чем больше амплитуда входных колебаний. При наличии зоны нечувствительности нелинейность имеет вид, показанный на рис.1.6.
Четвертый вид нелинейных характеристик вызывается наличием люфта или сухого трения в элементе. Вид такой нелинейной характеристики и простейшая механическая модель, поясняющая явление люфта и сухого трения, показаны на рис.1.7 и рис.1.8.
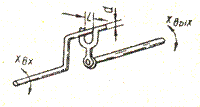
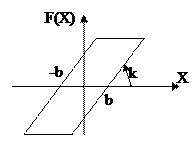
Рис.1.7. Характеристика Рис.1.8. Механическая
элемента с сухим трением модель элемента
Модель, изображенная на рис.1.9, отличается от модели, показанной на рис.1.8, только отсутствием фиксирующей пружины на ведомом валу. Эта на первый взгляд второстепенная конструктивная деталь существенно изменяет характер нелинейности. При изменении направления движения ведущего вала всегда (т. е. в любом положении обоих валов) происходит нарушение сцепления между валами, и движение ведомого вала в новом направлении начинается всякий раз только после перемещения на величину всего зазора в соединительной вилке. Аналитически такая нелинейная функция может быть записана следующим образом (за положительное направление вращения принято вращение вправо):
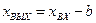 при
при 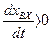
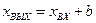 при
при 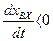
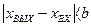 при
при 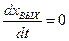
Нелинейности такого вида порождаются не только мертвыми ходами и зазорами в механических системах, но и, в частности, силами сухого трения между движущимися элементами механизмов. На рис.10 показана механическая система, в которой зона застоя обусловлена силами сухого трения.
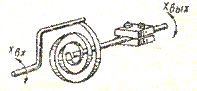
Рис.1.9. Зона застоя
обусловленная
силами сухого трения
Ведомый и ведущий валы связаны пружиной. Выходной вал зажат между тормозными колодками. Входной величиной является угол поворота ведущего вала, выходной — угол поворота ведомого вала. При вращении ведущего вала движение ведомого вала начинается только после того, как момент упругих сил закручиваемой пружины станет больше момента сил трения. Изменение направления движения ведомого вала, очевидно, может произойти только в том случае, если ведущий вал закрутит пружину в противоположную (совершающемуся движению) сторону на ту же величину. Ширина зоны застоя, таким образом, равна удвоенному значению момента сил трения, деленному на коэффициент упругости пружины (момент, развиваемый пружиной при закручивании ее на угол, равен единице).
Пятым видом нелинейных характеристик является релейная нелинейная характеристика с петлей возврата (рис.1.10).
| |
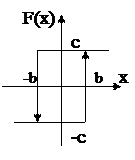
Рис.1.10. Релейная
гистерезис характеристика
с петлей возврата
Аналитическое выражение этой нелинейной функции для более общего случая, когда последняя располагается в верхней полуплоскости относительно оси, имеет следующий вид:
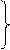
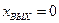 при
при 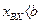
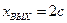 при
при 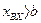 при
при 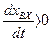
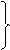
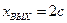 при
при 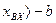
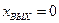 при
при 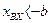 при
при 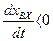
где b — значение входной величины, при котором происходит включение релейного элемента;
— b — значение этой же величины, при котором происходит отключение релейного элемента;
c — величина напряжения на контактах реле.
Подобный вид имеют статические характеристики реле. Наличие зоны возврата, т. е. разных значений тока трогания и тока опускания реле, объясняется рядом причин (креплением контактов реле на эластичных пружинах, различием в электрических характеристиках реле при разных положениях его якоря и т. д.).
Шестой вид нелинейных характеристик называется зоной нечувствительности второго рода с петлей возврата (рис. 1.11).
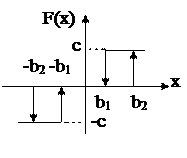
Рис. 1.11. Зона нечувствительности
второго рода с петлей возврата
Нелинейную функцию, характеризующую этот вид, в аналитической форме можно представить таким образом:
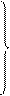
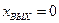 при
при 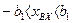
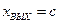 при
при 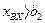 при
при 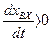
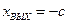 при
при 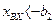
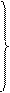
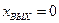 при
при 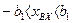
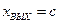 при
при 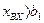 при
при 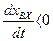
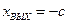 при
при 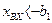
где b1 — абсолютное значение входной величины, при котором происходит включение реле в ту или иную сторону;
b2 — абсолютное значение входной величины, при котором происходит выключение релейного элемента;
c — амплитуда колебаний выходной величины (например, напряжение на контактах реле).
Подобные характеристики имеет, например, трехпозиционное поляризованное реле при симметричной настройке.
Кроме рассмотренных нелинейных характеристик, ниже приведены нелинейные характеристики: непрерывная (рис.1.12), идеальная релейная (рис.1.13), состоящая из отдельных отрезков прямых линий (рис.1.14):
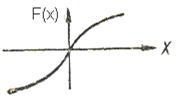
Рис. 1.12. Непрерывная
характеристика
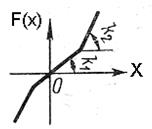
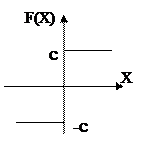
Рис. 1.13. Релейная Рис. 1.14. Характеристика
характеристика состоящая из отдельных
отрезков прямых линий
Можно различать статические и динамические нелинейности.
Статические нелинейности – это нелинейности статических характеристик(например, сухое трение (рис.1.7) зона нечувствительности (рис.1.1 рис.1.3 рис.1.6) , люфт (рис.1.7), гистерезис (рис.1.15), насыщение (рис.1.5), опережающая(рис.1.16), различные нелинейные функции).
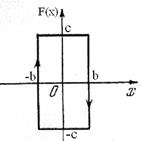
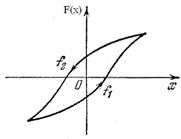
Рис.1.15. Гистерезисная Рис. 1.16. Опережающая характеристика характеристика
Динамические нелинейности — это нелинейности, связанные с дифференциальными уравнениями динамикизвена. К ним относится, например, нелинейное трение.
Так, нелинейная сила вязкого трения 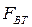 характеризуется выражением
характеризуется выражением
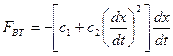
Сила сухого трения 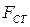 в простейшем случае (имеются и более сложные зависимости) описывается соотношением
в простейшем случае (имеются и более сложные зависимости) описывается соотношением
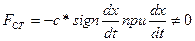
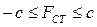 при
при 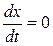
Звено с изменяющейся постоянной времени имеет вид
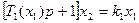
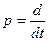
Здесь надо отметить особенность такой динамической нелинейности по сравнению с линейным звеном с переменным параметром вида
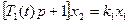
В системе с переменными параметрами фигурирует зависимость коэффициентов от времени,в то время как нелинейность характеризует их зависимость от координат(или производных). Точно так же, например, гистерезис, (рис. 1.15) представляет собой нелинейное (координатное) запаздывание, в отличие от временного или инерционного в линейных системах. Аналогично на рис. 1.16 представлено нелинейное (координатное) опережение. Конечно, могут быть нелинейные звенья с переменным параметром, например вида
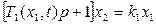
а также нелинейные запаздывающие звенья типа
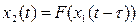
Примерами динамических нелинейностей могут служить также любые нелинейные дифференциальные, разностные и интегральные уравнения.
Нелинейности в системах управления и регулирования могут быть естественно присущимиреальной системе (трение, люфт, гистерезис, зона нечувствительности, насыщение) и зачастую вредными: влияние их в этом случае надо стремиться уменьшить. Но могут быть и специально вводимыенелинейности для придания системе желаемых свойств. Таковы, например, релейные элементы и различные нелинейные и псевдолинейные корректирующие устройства. Большой интерес представляют также логические нелинейные управляющие блоки и системы с переменной структурой, о которых речь будет в последующих главах. Оптимизация систем автоматического управления также в большинстве случаев связана с введением специальных нелинейностей в контур системы.
Введение специальных нелинейностей приводит к различным нелинейным законам управления, которые обладают более богатыми возможностями по сравнению с линейными.
Преобразования нелинейных статических характеристик
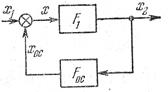
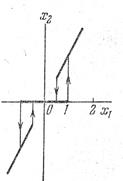
Поскольку нелинейности в системах чаще всего учитываются в виде статических характеристик, то целесообразно рассмотреть методы их преобразования. Такие преобразования обычно выполняют с целью объединения смежных нелинейных звеньев для упрощения проводимых исследований. Смежные звенья с нелинейными статическими характеристиками могут встречаться в схемах в виде последовательного соединения, согласно-параллельного соединения и встречно-параллельного соединения или обратной связи (рис.1.17).
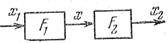
При последовательном соединении двух звеньев с нелинейными статическими характеристиками (рис. 1.17,а) для результирующей характеристики можно записать
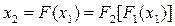 (1.1)
(1.1)
Это означает, что результирующая характеристика может быть получена как нелинейная функция 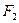 от выражения, стоящего в квадратных скобках, которое само является нелинейной функцией:
от выражения, стоящего в квадратных скобках, которое само является нелинейной функцией:
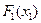 (1.2)
(1.2)
а) б) в)
Рис. 1.17. Смежные звенья с нелинейными
статическими характеристиками
Предположим, что первое звено имеет нелинейную статическую характеристику
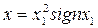
а второе звено — статическую характеристику
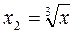
Тогда результирующая характеристика будет
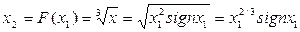
Если последовательно соединенные нелинейности заданы графически, то результирующая характеристика легко определяется графическим способом.
В качестве примера рассмотрим графическое построение результирующей характеристики 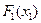 двух последовательно соединенных звеньев с нелинейными статическими характеристиками
двух последовательно соединенных звеньев с нелинейными статическими характеристиками 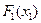 и
и 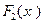 (рис. 1.18).
(рис. 1.18).
Ветвь первой характеристики строим, как обычно, в первом квадранте, а ветвь второй характеристики — во втором квадранте, принимая за ось абсцисс ось ординат первой характеристики. Интервал графического решения 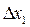 для переменной x1 выбираем таким, чтобы n дискретных значений переменных с достаточной точностью определяли исходные и искомую статические характеристики. Затем для каждого дискретного значения x1i находим точки ветви результирующей характеристики
для переменной x1 выбираем таким, чтобы n дискретных значений переменных с достаточной точностью определяли исходные и искомую статические характеристики. Затем для каждого дискретного значения x1i находим точки ветви результирующей характеристики 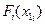 .
.
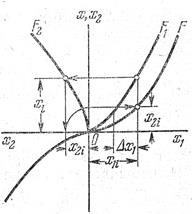
Рис.1.18. Графическое
решение для некоторого
значения 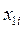
На рис. 1.18 показан порядок графического решения для некоторого значения 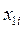 . Из точки соответствующей
. Из точки соответствующей 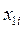 восстанавливаем перпендикуляр и определяем значение
восстанавливаем перпендикуляр и определяем значение 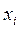 на характеристике
на характеристике 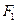 . Значение
. Значение 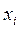 переносим (как показано стрелкой) на характеристику
переносим (как показано стрелкой) на характеристику 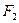 и, опустив перпендикуляр на ось абсцисс, получаем значение
и, опустив перпендикуляр на ось абсцисс, получаем значение 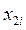 . Это значение
. Это значение 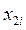 переносим на перпендикуляр, восстановленный из точки, соответствующей
переносим на перпендикуляр, восстановленный из точки, соответствующей 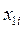 . Проделав такое построение для n значений, получим n точек, принадлежащих одной ветви статической характеристики
. Проделав такое построение для n значений, получим n точек, принадлежащих одной ветви статической характеристики 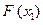 . Вторая ветвь функции
. Вторая ветвь функции 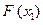 строится как кривая, симметричная первой ветви относительно начала координат.
строится как кривая, симметричная первой ветви относительно начала координат.
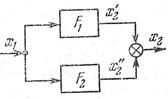
При согласно-параллельном включении звеньев с нелинейными статическими характеристиками (рис. 1.17, б) можно записать
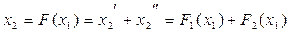 (1.3)
(1.3)
Получение результирующей статической характеристики здесь сводится к сложению статических характеристик отдельных звеньев и не представляет никакого затруднения как при аналитическом, так и графическом задании нелинейностей.
В случае встречно-параллельного соединения нелинейных звеньев (рис. 1.17, в) можно записать
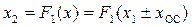
где знак «+» соответствует положительной обратной связи, а знак «—» — отрицательной. Так как
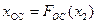
то получим
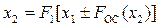
Разрешая последнее выражение относительно аргумента, имеем
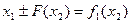
где 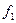 — функция, обратная
— функция, обратная 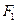 . Полученное выражение можно записать в виде
. Полученное выражение можно записать в виде
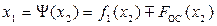 (1.4)
(1.4)
где 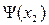 — результирующая функция, учитывающая сигналы прямой цепи и цепи обратной связи.
— результирующая функция, учитывающая сигналы прямой цепи и цепи обратной связи.
Искомая результирующая статическая характеристика контура будет функцией, обратной 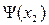 .
.
Как видно из (1.4), для получения результирующей статической характеристики нелинейного звена с нелинейной обратной связью следует найти функцию 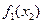 , обратную функции
, обратную функции 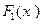 основного звена, вычесть (для положительной) или прибавить (для отрицательной обратной связи) нелинейную функцию обратной связи
основного звена, вычесть (для положительной) или прибавить (для отрицательной обратной связи) нелинейную функцию обратной связи 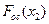 , а затем найти обратную функцию полученной суммарной функции
, а затем найти обратную функцию полученной суммарной функции 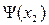 .
.
Пусть, например, имеем встречно-параллельное соединение двух звеньев с нелинейностями, заданными аналитически (рис. 1.19).
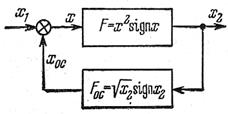
Рис.1.19. Встречно-параллельное
соединение двух звеньев
Согласно (1.4) запишем выражение входной величины системы с отрицательной обратной связью
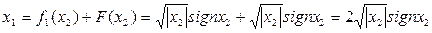
Разрешая полученное выражение относительно 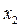 , получим результирующую статическую характеристику
, получим результирующую статическую характеристику
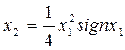
Если уравнение (1.4) трудно разрешимо относительно 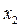 , то можно не находить аналитического выражения результирующей статической характеристики, а, задаваясь значениями
, то можно не находить аналитического выражения результирующей статической характеристики, а, задаваясь значениями 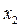 , определять
, определять 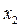 и строить характеристику графически.
и строить характеристику графически.
Таким же образом к одному звену можно приводить нелинейное звено, охваченное жесткой линейной связью, или линейное звено, охваченное жесткой нелинейной связью.
При графическом задании исходных нелинейных статических характеристик в случае встречно-параллельного соединения нелинейных звеньев построение результирующей характеристики эквивалентного звена согласно (1.4) может быть выполнено в следующем порядке. В координатных осях ( 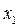 ,
, 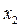 ) строится, как обычно, характеристика основного звена
) строится, как обычно, характеристика основного звена 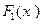 . Затем строится характеристика звена обратной связи, для которой переменная
. Затем строится характеристика звена обратной связи, для которой переменная 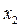 , откладываемая на оси ординат, является аргументом, а
, откладываемая на оси ординат, является аргументом, а 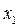 является функцией
является функцией 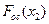 . Сложив значения
. Сложив значения 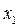 указанных характеристик в дискретных точках, получим результирующую характеристику для отрицательной обратной связи. Для положительной обратной связи из значений
указанных характеристик в дискретных точках, получим результирующую характеристику для отрицательной обратной связи. Для положительной обратной связи из значений 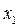 на характеристике
на характеристике 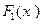 следует вычесть значения
следует вычесть значения 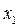 характеристики обратной связи
характеристики обратной связи 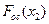 .
.
Полученная характеристика и будет эквивалентной результирующей
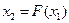
В качестве примера рассмотрим получение результирующей характеристики для основного звена, имеющего статическую характеристику с зоной нечувствительности при линейном продолжении (рис. 1.20, а), и звена обратной связи, имеющего характеристику с ограничением.
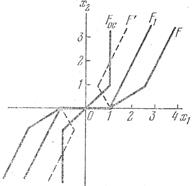
а) б) в)
Рис.1.20. Получение результирующей
характеристики для основного звена
Характеристику основного звена 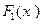 строим, как обычно, на координатной плоскости (
строим, как обычно, на координатной плоскости ( 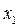 ,
, 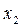 ) (рис. 1.20, б), принимая
) (рис. 1.20, б), принимая 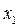 за переменную х. Характеристику
за переменную х. Характеристику 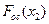 строим в зависимости от своего аргумента
строим в зависимости от своего аргумента 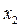 . Сложив значения
. Сложив значения 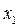 для построенных характеристик, получим результирующую характеристику
для построенных характеристик, получим результирующую характеристику 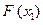 для случая отрицательной обратной связи. Вычтя значения
для случая отрицательной обратной связи. Вычтя значения 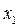 для
для 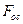 из значений
из значений 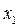 для
для 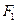 получим характеристику для положительной обратной связи
получим характеристику для положительной обратной связи 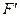 (пунктирная ломаная).
(пунктирная ломаная).
Интересно отметить, что полученная результирующая характеристика при положительной обратной связи 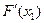 в интервале
в интервале 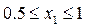 имеет двузначность, а в точках
имеет двузначность, а в точках 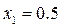 и
и 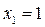 будет иметь место релейный эффект. Практически эквивалентная статическая характеристика будет релейной с линейным продолжением (рис. 1.20, в).
будет иметь место релейный эффект. Практически эквивалентная статическая характеристика будет релейной с линейным продолжением (рис. 1.20, в).
Дата добавления: 2020-10-25; просмотров: 1243;











