Составление уравнений нелинейных автоматических систем
Составление уравнений нелинейных автоматических систем обычно производится после построения структурных схем. Как и при исследовании линейных систем, вначале составляются уравнения отдельных звеньев, а затем эти уравнения объединяются в уравнение системы. Заметим, что некоторые методы исследования (методы моделирования, графоаналитические методы) не требуют перехода от уравнений звеньев к уравнению системы.
Наличие нелинейных звеньев не позволяет получить сразу единое уравнение нелинейной системы. В простейшем случае, как отмечалось, система представляется в виде линейной части с ее линейным дифференциальным уравнением и нелинейности, описываемой либо нелинейным дифференциальным или алгебраическим уравнением, либо графиком нелинейной статической характеристики. Рассматриваемые здесь методы исследования в основном и базируются на представлении системы в виде линейной части и нелинейности.
При объединении линейного уравнения линейной части и нелинейного уравнение (для нелинейности) общее уравнение системы будет нелинейным. Получение линейного уравнения системы становится возможным лишь после применения к нелинейностям методов линеаризации. Применение для анализа и синтеза нелинейных систем амплитудно-фазочастотных характеристик позволяет выполнить исследование процессов в замкнутых системах по их характеристикам в разомкнутом состоянии. Поэтому переход к единому уравнению замкнутой системы часто и не требуется.
Уравнения линейных звеньев составляются по известным методам линейной теории. Для нелинейных звеньев уравнения записываются в виде нелинейных функций. Здесь будем использовать в основном готовые уравнения динамических звеньев, известные из литературы. К подробному составлению уравнений звеньев будем прибегать лишь в некоторых случаях при рассмотрении конкретных примеров нелинейных систем.
Составление уравнений линейных частей системы может выполняться либо методом исключения переменных, либо с помощью передаточных функций линейных звеньев, объединенных в линейную часть системы (при этом должны выполняться правила структурных преобразований для линейных систем).
Пусть требуется составить уравнение для одноконтурной системы с одним нелинейным звеном (рис. 1.21), с внешним задающим воздействием 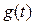 и выходной переменной
и выходной переменной 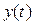 .
.
В соответствии со структурной схемой можно записать:
уравнение датчика рассогласований
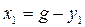 (1.5)
(1.5)
уравнение первого звена
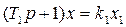 (1.6)
(1.6)
уравнение нелинейного звена
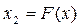 (1.7)
(1.7)
уравнение третьего звена
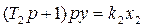 (1.8)
(1.8)
уравнение звена обратной связи
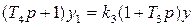 (1.9)
(1.9)
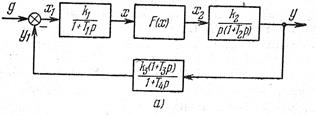
Рис.1.21,а. Одноконтурная
система с одним
нелинейным звеном
Найдем уравнение линейной части методом исключения переменных. Выходной величиной линейной части является переменная х, и поэтому, начиная с первого звена, исключаем переменные, обходя контур против направления прохождения сигналов. Заменяя в уравнении (1.6) 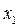 его значением из (1.5), имеем
его значением из (1.5), имеем
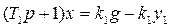 (1.10)
(1.10)
Умножая полученное уравнение на оператор 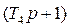 левой части уравнения (1.9), исключаем переменную
левой части уравнения (1.9), исключаем переменную 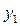 :
:
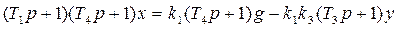
Далее полученное уравнение умножаем на оператор 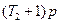 левой части уравнения (1.8) и исключаем переменную у:
левой части уравнения (1.8) и исключаем переменную у:
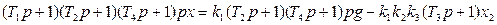 (1.11)
(1.11)
В результате получаем дифференциальное уравнение линейной части системы с ее выходной переменной х, входной переменной х2 и задающим воздействием g.
Объединяя (1.7) и (1.11), т. е. исключая переменную 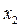 , получаем нелинейное уравнение замкнутой системы для входной переменной нелинейного звена
, получаем нелинейное уравнение замкнутой системы для входной переменной нелинейного звена
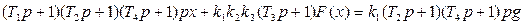 (1.12)
(1.12)
Здесь в процессе составления общего уравнения системы исключилась выходная переменная системы 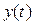 , которая может интересовать нас при исследовании. После получения решения уравнения (1.40) для переменной
, которая может интересовать нас при исследовании. После получения решения уравнения (1.40) для переменной 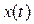 можно всегда пересчитать решение к выходной величине системы
можно всегда пересчитать решение к выходной величине системы 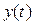 через передаточные функции звеньев, разделяющих
через передаточные функции звеньев, разделяющих 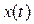 и
и 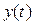 , или с помощью выражений (1.9) и (1.10).
, или с помощью выражений (1.9) и (1.10).
Если в нелинейной системе составлять уравнение сразу относительно выходной величины, то оно, как правило, до конца не разрешается, так как выходная величина входит в аргумент нелинейной функции. Действительно, взяв уравнение (1.8) за исходное, можно в нем вместо 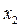 подставить его значение (1.7). Тогда будем иметь
подставить его значение (1.7). Тогда будем иметь
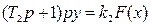
Далее следует исключить переменную х. Взяв ее значение из (1.6), будем иметь
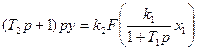
Заменив 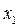 его значением (1.5), получим
его значением (1.5), получим
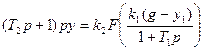
Учитывая значение 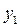 из (1.9), последнее выражение можно записать в виде
из (1.9), последнее выражение можно записать в виде
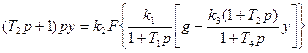 (1.13)
(1.13)
из которого очевидны трудности определения выходной переменной системы 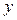 .
.
Таким образом, в нелинейных системах из-за наличия нелинейностей общее уравнение составляется не относительно выходной переменной системы, а относительно выходной переменной линейной части или относительно входной переменной нелинейного звена.
При рассмотрении собственного движения нелинейной системы уравнение линейной части можно сразу записать через передаточную функцию. После переноса сумматора через первое звено по ходу сигнала и переноса разветвления через третье звено против хода сигнала исходная структурная схема (рис. 1.21, а) преобразуется к виду, изображенному на рис. 1.21, б.
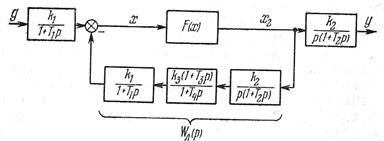
Рис.1.21.б. Преобразованная
одноконтурная
система с одним нелинейным звеном
Для рассматриваемого примера при 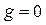 и временном неучете выходной переменной системы у передаточная функция линейной части системы будет равна
и временном неучете выходной переменной системы у передаточная функция линейной части системы будет равна
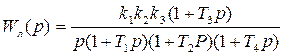
откуда имеем
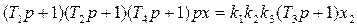 (1.14) что соответствует (1.39) при
(1.14) что соответствует (1.39) при 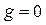 и учете знака «—», необходимого для замыкания системы.
и учете знака «—», необходимого для замыкания системы.
В качестве второго примера составим уравнение нелинейной системы, имеющей жесткую дополнительную обратную связь, охватывающую нелинейное звено (рис. 1.22).
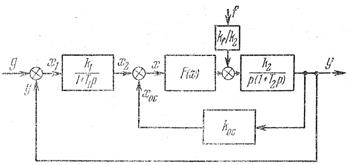
Рис.1.22. Нелинейная система
с жесткой дополнительной
обратной связью
Запишем уравнения звеньев системы соответственно их передаточным функциям:
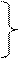
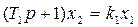
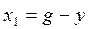 (1.15)
(1.15)
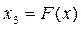 (1.16)
(1.16)
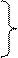
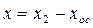
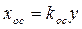 (1.17)
(1.17)
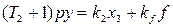 (1.18)
(1.18)
Коэффициент 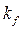 , связывает изменение скорости
, связывает изменение скорости 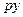 с возмущением
с возмущением 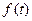 .
.
Составим уравнение линейной части, в которую включаем все звенья и узлы системы, кроме нелинейного звена. Для линейной части выходной величиной является переменная х, а входной — переменная 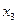 . Из (1.17) имеем
. Из (1.17) имеем
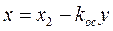
Умножив данное уравнение на оператор левой части уравнения (1.15), получим
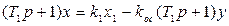
или при учете соотношения замыкания системы: 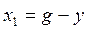
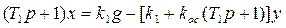
Полученное уравнение умножаем на оператор левой части, уравнения (1.18). Тогда имеем
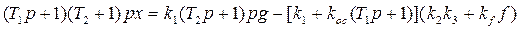
или окончательно
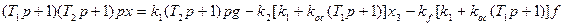
Полученное линейное уравнение линейной части может быть объединено с уравнением нелинейного звена (1.16) в единое нелинейное уравнение замкнутой системы.
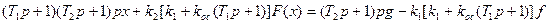
Дата добавления: 2020-10-25; просмотров: 621;











