Следует еще раз обсудить вопрос: почему так важна степень формализации процедуры коллективной экспертизы?

Во-первых – уже было отмечено, что более формализованная модель дает более надежные результаты. Во-вторых – чем менее формализован алгоритм экспертной оценки, тем выше должна быть квалификация экспертов, и тем дороже обойдутся инвестору их услуги. Следовательно, более надежно и менее затратно заключение, подготовленное по детально проработанному алгоритму. В-третьих, чем менее формализован алгоритм экспертной оценки, тем труднее инвестору сопоставить между собой различные проекты, чтобы отобрать наиболее выгодный (более доходный и менее рискованный). Следовательно, шансы ошибиться в выборе проекта у инвестора выше при слабой формализации процедуры экспертизы. Из сказанного следует, что алгоритм оценки должен учитывать 2 группы рисков: собственные риски проекта и риски ошибок экспертов.

Один из возможных вариантов такого алгоритма был разработан и практически применялся в Фонде финансовой поддержки малого предпринимательства (ФФПМП) при Торгово-промышленной палате Республики Татарстан (ТПП РТ). Рассмотрим поэтапно алгоритм оценки совокупного риска проекта по этой методике.

1 этап.Эксперты изучают проект, и каждый заполняет анкету, содержащую около 40 вопросов по основным мероприятиям и факторам риска. Ответ на вопрос анкеты – это не что иное, как вербальная модель механизма действия какой-то совокупности факторов риска. Факторы риска сведены в 2 группы: факторы, связанные с неадекватностью проектных решений и факторы, связанные с недостоверностью информации. По каждому мероприятию проекта дается две оценки в баллах по специальным шкалам. Шкала оценки адекватности решений по мероприятию (a_i ) отражает способность обеспечить достижение запланированных результатов:

0 – мероприятие необходимо, но в проекте отсутствует;

1 – мероприятие предусмотрено, но требует полной переработки;

2 – мероприятие требует значительной переработки;

3 – мероприятие требует доработки (дополнения);

4 – мероприятие требует незначительной доработки;

5 – мероприятие полностью соответствует целям проекта.

Шкала оценки достоверности информации по мероприятию (д_i )

-1 – информация случайно или умышленно искажена и противоречит первичным документам проекта или документам, которыми располагает эксперт;

0 – информация не имеет документального подтверждения;

+1 – информация имеет косвенное подтверждение в документах;

+2 – информация имеет прямое подтверждение в документах.

2 этап.Подсчитываются суммы баллов А = Σ a_i и Д = Σ д_i и рассчитывается относительный уровень адекватности и достоверности проекта в целом А_отн = А / А_maxиД_отн = Д / Д_max. Здесь А_max и Д_max – максимально возможные суммы баллов по двум шкалам (оценка идеального проекта).

3 этап.Рассчитывается вероятность достижения ожидаемого результата проекта В_ор. Для Фонда таким результатом, косвенно подтверждающим коммерческий успех проекта, являлся возврат кредита и уплата процентов. В_ор = А_отн ^1/n Д_отн ^1/m, здесь параметры0<m<1 и 0<n<1 отражают качество экспертизы (чем выше показатели, тем лучше организована экспертиза, тем меньше риск ошибки эксперта).

Проверим эмпирическую формулу оценки вероятности В_ор на логичность. Допустим, методика балльной оценки мероприятий (анкета эксперта) близка к идеальной, а эксперт практически непогрешим. Тогда m » n » 1.

Допустим, есть неплохой по меркам ФФПМП проект, у которого А_отн =0,7 и Д_отн =0,9. Тогда В_ор = 0,63 (риск 37%). Теперь допустим, что есть другой, просто отличный проект, у которого А_отн =0,99 и Д_отн =0,99.Для этого проекта В_ор = 0,99 ^1/1 0,99 ^1/1 » 0,98 (риск 2%), что полностью соответствует исходной гипотезе. И вот теперь пусть теперь этот отличный проект оценит самый слабый эксперт, который почти ничего не понимает в проекте и при этом пользуется самой скверной методикой оценки. Тогда m → 0 и n → 0, а В_ор = 0,99 ^{1/ 0} 0,99 ^{1/ 0} = 0,99^∞ 0,99^∞ → 0.

Из-за предельно низкого качества экспертизы риск для инвестора возрастает до 100% ! На практике это, конечно, абсурдный случай, но сейчас для нас важна логичность результата расчета в рамках сделанных предположений. Реально всегда m > 0 и n > 0. Но как определить качество экспертизы? Как рассчитать эти m и n ?

Качество экспертизы можно определить только путем сравнения прогнозных экспертных оценок и действительных результатов реализации проектов. Нужно убедиться: действительно ли проекты, по которым эксперты ставили низкие баллы А и Д , проваливались чаще, а те, риск которых был оценен как незначительный, чаще завершались успешно? Таким образом, нужно статистически обосновать значения m и nпо уровню сбываемости экспертных прогнозов.

За 3,5 года ФФПМП профинансировал 87 проектов с различными уровнями А_отн и Д_отн . Часть из них (около 10) провалилась и на этой статистической основе по расчетам оказалось m = 0,83иn = 0,41(достоверность эксперту оценить легче, требуется меньшая квалификация, чем для оценки адекватности мероприятий). Заметим в заключение, что формула В_ор =А^1/n Д^1/m не агрегирует вероятности успеха по отдельным мероприятиям, они в этой методике не определяются. В методике используется статистически наблюдаемая связь (корреляция) между итоговыми балльными оценками достоверности и адекватности с одной стороны, и фактическими результатами реализации множества проектов, по которым такие оценки были в свое время даны.

Модуль 3.3. Способы учета проектных рисков в анализе денежных потоков проекта

Допустим, надежность проекта в целом оценена, доходность проекта по денежным потокам установлена.

В Гипермодуле 1 был рассмотрен пример сопоставления уровня доходности и надежности проекта. На одной шкале – доходность проекта, на другой – риск как вероятность его провала в %. Как их соизмерить? Как определить, какой суммой ожидаемого дохода инвестор согласен пожертвовать за каждый дополнительный процент повышения вероятности успеха?

Наиболее часто для этого применяется способ внесения поправки на риск проекта в ставку дисконта d. Смысл такой поправки в том, чтобы заложить в алгоритм расчета ЧДД требование генерировать дополнительный доход, который по расчетам покрыл бы потенциальные убытки, вызванные факторами риска. Часто этот дополнительно требуемый доход называют премией за риск инвестора.

Допустим, инвесторам предложено профинансировать 20 весьма надежных проектов, каждый длительностью 1 год и капиталоемкостью К_о=100. По расчетам у всех проектов ВНД близка к 10%, а их совокупный годовой доход составляет, таким образом, 100х20х(1+0,1) = 2200. Инвесторы дали предварительное согласие, но попросили оценить риски проекта.

К моменту проведения экспертизы макроэкономическая ситуация изменилась и эксперты установили, что в новых условиях риск полного провала для подобных проектов составляет около 5% . Иначе говоря,1 из 20 проектов «статистически достоверно» закончится потерей вложенного в него капитала (100 единиц) и недополучением дохода (10 единиц).

Теперь совокупный годовой доход по группе проектов ожидается в сумме 2090, что соответствует ВНД = 4,5%. Это инвесторов не устраивает.

Инвесторы согласятся профинансировать проекты, если в них будут внесены изменения, которые увеличат ожидаемый доход от совокупных вложений на 110 единиц. При этом сохраняется исходная инвестиционная емкость совокупности проектов 2000, а уровень общего риска каждого из проектов составит около r = 5%.

Таким образом, ВНД должна увечиться на 5,5% (110/2000), то есть возрасти от 10% до 15,5% . Эта дополнительная доходность воспринимается инвесторами как справедливая премия за риск. Так логически обосновывается один из возможных способов учета проектных рисков. Остается эту дополнительную доходность добавить к доходности безрисковых альтернативных вложений d при расчете ставки дисконтирования δ. Расчет выглядит следующим образом: (1+δ _r ) = (1+d)(1 + r) = (1+ d + r + d r ). Часто последним «довеском» пренебрегают ввиду малости слагаемого и упрощенно считают, что δ _r = d + rиα_tr = (1+ d + r) ^-t. При таком расчете убытки в сумме (100+10), связанные с ожидаемым провалом 1 из 20 рискованных проектов, почти полностью покроются «премиальным» доходом. Этот доход будет равен 95+ 9,5 (это 5% + 0,5% от 1900), а весь требуемый инвестором возврат вложений через год с учетом риска составит 1900 + 1900*0,1 + 1900*0,05 + 1900*0,005 = 2194,5 (т.е. почти все ожидавшиеся 2200).

Отметим 4 обстоятельства, о которых должен помнить эксперт, использующий этот метод учета риска.

1. В результате премиальной поправки ставка дисконта увеличивается, и более рискованный, но равно доходный с депозитом по денежным потокам проект при тех же расчетных значениях недисконтированных финансовых результатов(ФР_t) имеет меньший ЧДД. То есть по этому формальному показателю проект выглядитдля инвестора менее привлекательно, чем столь же доходный, но безрисковый депозит. Это значит, что поправка r не меняет сущности самого проекта, а просто сводит к единому формальному показателю ЧДД две самостоятельных характеристики проекта – его доходность и надежность

Другими словами, поправка дает возможность сравнивать рискованный проект с безрисковым депозитным вкладом по известным формальным показателям ЧДД_Т или t _ОК

2. По мере увеличения рискованности проектов добавка к ставке дисконта рассчитанная по формуле δ _r = d + r,все менее точно отражает в показателе ЧДД ожидаемые потери. Мы видели, что уже при риске 5% нет полного возмещения потенциальных потерь: 2194,5 ≈ 2200.

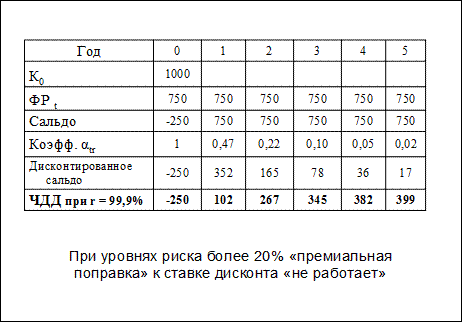
Допустим, при весьма высокой ожидаемой доходности риск проекта 99,99%, т.е. проект наверняка провалится, и капитал наверняка будет потерян. Логично ожидать, что расчетное значение ЧДД_Т с поправкой на риск проекта должно быть отрицательным

Однако если простой (без дисконтирования) срок окупаемости пятилетнего проекта составит менее 2 лет, то, применяя коэффициент α_t = (1+ 0,14 + 0,9999) ^–t , можно и в этом случае получить вполне убедительно ЧДД_Т=5 > 0 и по формальному признаку этот проект может быть профинансирован!!!

Вывод таков: «премиальная» поправка имеет эмпирический характер, и подтверждается реальным опытом инвестирования проектов с рисками в диапазоне до 15-20% . При больших уровнях риска теория премирования за риск «не работает» .

Можно предложить и теоретически обосновать другие варианты корректировки показателя ЧДД на совокупный риск проекта. Например, можно обосновать расчет коэффициента дисконтирования по формуле α*_tr = (1- r) ^t (1+ d) ^–t (предполагается, что уровень риска одинаков по интервалам, а результатом деятельности является либо получение ожидаемого дохода, либо его отсутствие – третьего не дано!)

При таких предположениях вероятность полной потери доходов в 1-м интервале расчетного периода, то есть вероятность получения ФР₁^п = 0, равна r, а вероятность противоположного события, то есть вероятность получения ожидаемого планового результата ФР₁ равна В_ОР1 = (1- r). Следовательно, математическое ожидание результата за 1-й расчетный интервал (средняя вероятная величина) составит сумму ФР₁^. (1- r) + ФР₁^{п .} r = 0 + ФР₁^. (1- r).

Вероятность того, что проект не провалился ни в первом , ни во втором интервале и даст ожидаемый результат ФР₂, по правилу произведения вероятностей двух зависимых событий составит (1- r) ^. (1- r) = (1- r)² , а вероятность полной потери доходов, т.е. получения нулевого результата именно во втором интервале ФР₂^п = 0, равна произведению вероятности успеха в первом интервале (1- r) и вероятности провала во втором интервале r, то есть (1- r) ^. r.

Таким образом, математическое ожидание результата за второй интервал составит ФР₂^. (1- r) ² + ФР₂^{п .} (1- r) ^. r = ФР₂^. (1- r) ² , а за любой t –й интервал она составит ФР_t^. (1- r) ^t + ФР_t^{п .} r = ФР_t^. (1- r) ^t , что и требовалось доказать.

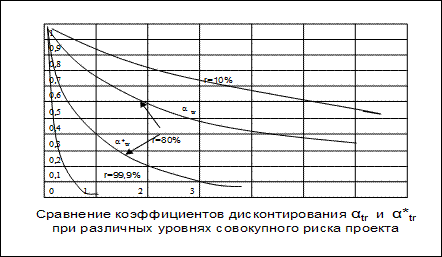
Для наглядности сравним графики при двух методах корректировки ЧДД. Видно, что в диапазоне риска до 10% кривые α_{tr и} α*_tr практически совпадают, но при более высоких уровнях риска (80%) значительно расходятся. При риске 99,9% уже на первом шаге t =1 α*_tr = 0, что подтверждает нецелесообразность финансирования проекта.

Наконец, последние два обстоятельства из заявленных четырех, которые касаются любого способа учета риска путем введения поправок в формулу расчета коэффициента дисконтирования.

3. Если в какой-то последовательности интервалов ожидаемое сальдо денежных потоков отрицательно (например, в инвестиционной фазе), то применение коэффициентов α_tr или α*_tr в этих интервалах приведет не к снижению ЧДД, а к его увеличению по сравнению с расчетом по обычной ставке дисконта, что противоречит самой идее отражения риска через снижение ЧДД.

4. Рассмотренные методы не позволяют учитывать степень риска по отдельным мероприятиям, а учитывает сразу совокупную степень риска проекта в целом.

Этих недостатков лишен способ учета рисков в денежных потоках с помощью создания резервов, мобилизация которых в процессе реализации проекта позволяет преодолеть угрозы провала проекта.

С точки зрения воздействия на ЧДД такой способ учета также ведет к снижению этого формального показателя, поскольку увеличивает денежные оттоки. Рассмотрим этот более сложный способ учета рисков в Гипермодуле 4.

Контрольные задания по материалу Гипермодуля 3

Контрольное задание 1: через несколько месяцев ваш личный проект под названием «Диплом бакалавра» должен перейти в эксплуатационную фазу и начать приносить доход. Какие внешние и внутренние факторы риска могут помешать его успешному завершению?

Контрольное задание 2: приходилось ли вам принимать жизненно важные решения на основе чужого экспертного мнения? Чем завершилось дело? Приведите пример.

Контрольное задание 3: какие отличия в моделях оценки риска по методике ФФПМП ТПП РТ и в деловой игре «6-й регион-К» вы можете указать ?

Контрольное задание 4: приведите примеры из вашей жизни, когда в обычных «житейских» ситуациях вам пришлось соразмерять свои денежные расходы с риском утраты или неполучения ценностей, не поддающихся денежному измерению.

Контрольное задание 5: на каких гипотезах (предположениях) фактически основана поправка на риск в коэффициенте дисконтирования, рассчитанном по формуле α*_tr = (1- r) ^t (1+ d) ^–t ? Насколько справедливы эти предположения ?