Спецификация модели

Регрессия представляет собой зависимость среднего значения какой – либо величины от некоторой другой величины или от нескольких величин. В отличие от функциональной зависимости, когда каждому значению независимой переменной х соответствует одно определенное значение величины y, при регрессионной связи одному и тому же значению х могут соответствовать в зависимости от случая различные значения величины y.

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными – y и x, то есть модель вида:

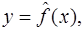
(1)

где y – зависимая переменная (результативный признак); x - независимая, или объясняющая переменная (признак – фактор, или регрессор).

Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, то есть модель вида:

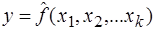
(2)

Любое эконометрическое исследование начинается со спецификации модели, то есть с формулировки вида модели, исходя из соответствующей теории связи между переменными.

Из всего круга факторов, влияющих на результативный признак, необходимость выделить наибольшие существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Например, выдвигается гипотеза о том, что величина спроса y на товар находится в обратной зависимости от цены x, то есть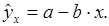

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как закономерность лишь в среднем по совокупности наблюдений. (Например, если зависимость спроса y от цены x: 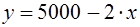означает, что с ростом цены на 1 д.е. спрос в среднем уменьшается на 2 д.е.).

В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи. В каждом отдельном случае величина y складывается из двух слагаемых:

,

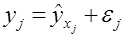где 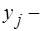фактическое значение результативного признака; 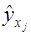- значение признака, найденное из математической функции связи y и x, то есть из уравнения регрессии; 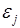- случайная величина, характеризующая отклонение реального значения признака от найденного по уравнению регрессии.

Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее порождают 3 источника: спецификация модели, выборочный характер исходных данных и ошибки измерения.

Ошибки спецификации. Это прежде всего неправильно выбранная форма модели. В частности, зависимость спроса от цены может быть выражена линейно

,

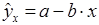но возможны и другие соотношения, например

, , .

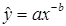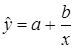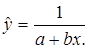Ошибки спецификации тем меньше, чем в большей мере теоретические значения признака подходят к фактическим данным y.

К ошибкам спецификации относится также недоучет в уравнении регрессии какого-либо существенного фактора, то есть использование парной регрессии вместо множественной. Например, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения.

Ошибки выборки. Исследователь при установлении связи между признаками имеет дело с выборочными данными. При изучении экономических процессов данные в исходной совокупности часто являются неоднородными. В этом случае уравнение регрессии не имеет практического смысла. Поэтому для получения хорошего результата из выборки исключают единицы с аномальными значениями исследуемых признаков.

Ошибки измерения. Представляют наибольшую опасность в практическом использовании методов регрессии. Ошибки спецификации можно уменьшить, изменяя форму модели, ошибки выборки - увеличивая объем исходных данных, ошибки измерения сводят на нет все усилия по количественной оценке связи между признаками. Например, статистическое измерение дохода на душу населения может иметь ошибку в результате наличия сокрытых доходов.

В эконометрических исследованиях предполагается, что ошибки измерения сведены к минимуму. Поэтому основное внимание уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции (1) может быть осуществлен тремя методами: графическим, аналитическим и экпериментальным.

Графический метод достаточно нагляден. Он основан на поле корреляции. Рассмотрим типы кривых.

Используются и другие типы кривых:

; ; ;

; ; .

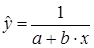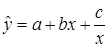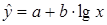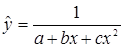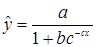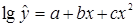Аналитический метод выбора типа уравнения регрессии основан на изучении материальной природы связи исследуемых признаков.

Пусть, например, изучается потребность предприятия в электроэнергии y в зависимости от объема выпускаемой продукции x. Все потребление электроэнергии можно подразделить на 2 части:

- не связанное с производством продукции a;

- непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее с увеличением объема выпуска bx;

Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида

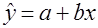
Разделив на x, получим удельный расход электроэнергии на единицу продукции :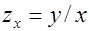

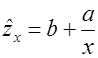
Это равносторонняя гипербола.

Экспериментальный метод используется при обработке информации на компьютере путем сравнения величины остаточной дисперсии 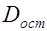, рассчитанной на разных моделях. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии факторов:

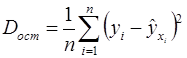
Чем меньше 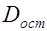, тем меньше наблюдается влияние прочих факторов, тем лучше уравнение регрессии подходит к исходным данным. При обработке данных на компьютере разные математические функции перебираются в автоматическом режиме, и из них выбирается та, для которой 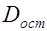является наименьшей.

Если 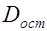примерно одинакова для нескольких функций, то на практике выбирают более простую, так как она в большей степени поддается интерпретации и требует меньшего объема наблюдений. Результаты многих исследований подтверждают, что число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной x. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений. Для рядов динамики, ограниченных по протяженности – 10, 20, 30 лет – предпочтительна модель с меньшим числом параметров при x.