Метод аналитического выравнивания

Для того, чтобы представить количественную модель, выражающую общую тенденцию изменений уровней динамического ряда во времени, используетсяаналитическое выравнивание ряда динамики. В этом случае фактические уровни заменяются уровнями, вычисленными на основе определенной кривой. Предполагается, что она отражает общую тенденцию изменения во времени изучаемого показателя.

При аналитическом выравнивании ряда динамики закономерно изменяющийся уровень изучаемого показателя оценивается как функция времени, то есть уровни динамического ряда вычисляются по соответствующему аналитическому уравнению на момент времени .

Для характеристики связей экономических показателей используют следующие типы функций:

• линейную

• гиперболическую

• показательную

• параболическую

• степенную

• логарифмическую

• логистическую

Основанием для выбора вида кривой может использоваться содержательный анализсущности развития данного явления. Можно опираться также на результаты предыдущих исследований в данной области. На практике для этих целей прибегают к анализу графического изображения уровней динамического ряда. При выборе формы уравнения следует исходить и из объема имеющейся информации. Чем больше параметров содержит уравнение тренда, тем больше должно быть наблюдений при одной и той же степени надежности оценивания.

Выбор формы кривой может осуществляться на основе принятого критерия, в качестве которого может служить сумма квадратов отклонений фактических значений от значений, рассчитанных по уравнению тренда. Из совокупности кривых выбирается та, которой соответствует минимальное значение критерия.

Рассмотрим аналитическое выравнивание ряда динамики по прямой, т.е. аналитическое уравнение вида:

Параметры a₀ и a₁ прямой рассчитываются по методу наименьших квадратов (МНК). Система нормальных уравнений для нахождения параметров в данном случае имеет вид:

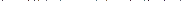
Поиск параметров уравнения можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю. При нечетном числе уровней ряда динамики уровень, находящийся в середине ряда, принимается за условное начало отсчета времени (этому периоду или моменту времени придается нулевое значение). Даты времени, стоящие ранее этого уровня, обозначаются натуральными числами со знаком минус (-1,-2,-3 и т.д.), а позже - натуральными числами со знаком плюс (+1, +2, +3 и т.д.)

Тогда получим:

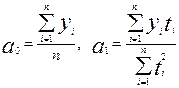
Рассмотрим аналитическое выравнивание ряда динамики по линейной зависимости cтроительствa жильяжилищно-строительными кооперативами Россииза 1990-1994 гг.(табл.2.13)

Таблица 2.13

Аналитическое выравнивание ряда динамики по прямой

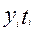
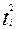
Годы	Построено, млн. кв.м, y	Условное время t			Выравнен-ные уровни ряда
	2,9	-2	-5,8		2,76
	2,4	-1	-2,4		2,49
	2,1				2,22
	1,9		1,9		1,95
	1,8		3,6		1,68
					1,41
Итого	11,1		-2,7		11,10

Используя таблицу определим параметры уравнения прямой

Уравнение прямой ряда динамики:

Подставив в это уравнение t =3, получим прогноз на следующий год в объеме 1.41 млн. руб жилья, построенного жилищно-строительными кооперативами.

Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. Возможность экстраполяции обеспечивается двумя обстоятельствами:

1) общие условия, определяющие тенденцию развития в прошлом, не претерпевают существенных изменений в будущем;

2) тенденция развития явления характеризуется тем или иным аналитическим уравнением.

При составлении прогнозов оперируют не точечной, а интервальной оценкой, определяя так называемые доверительные интервалы прогноза. Величина доверительного интервала определяется в общем виде так:

где среднее квадратическое

отклонение от тренда

t_a,n-m- табличное значение - критерия Стьюдента при уровне значимости а;

n - число уровней ряда;

m- количество параметров в уравнении тренда (для уравнения прямой m = 2).

Следует помнить, что прием аналитического выравнивания содержит в себе ряд условностей, связанных прежде всего с тем, что уровни, характеризующие тот или иной динамический ряд, рассматриваются как функция времени. В действительности же развитие явлений обусловлено не тем, сколько времени прошло с отправного момента, а тем, какие факторы влияли на развитие, в каком направлении и с какой интенсивностью. Развитие явлений во времени выступает как внешнее выражение этих факторов, как их суммарное действие, оказывающее влияние на изменение уровня в отдельно взятые промежутки или моменты времени.

Выявить основную тенденцию развития явления методом наименьших квадратов можно лишь тогда, когда выяснено, что изменяющиеся во времени процессы протекают на всем рассматриваемом промежутке времени одинаково, что их количественное и качественное изменение происходит под действием одного и того же комплекса основных факторов, определяющих движение данного ряда динамики. Экстраполяция на отдаленные даты подвержена более значительным ошибкам, чем краткосрочная экстраполяция.