Средние характеристики ряда динамики

Для обобщающей характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели. Рассмотрим две категории этих показателей:

1) средние уровни ряда,

2)средние показатели изменения уровней ряда.

Метод расчета среднего уровня ряда динамики зависит от вида временного ряда.

Для интервального ряда динамики абсолютных показателей средний уровень за период определяется по формуле простой средней арифметической:

,

где n- число уровней ряда.

Если предположить, что в течение времени уровень ряда остается неизменным, то средний уровень ряда рассчитывается по формуле средней арифметической взвешенной:

,

где t_i - промежуток времени между уровнями.

При определении средних уровней временного ряда нужно иметь в виду, что средняя будет достаточно надежной характеристикой ряда динамики, если она характеризует период с более или менее стабильными условиями развития.

Средний уровень моментного динамического ряда с равными (одинаковыми)промежутками времени между датами производится по формуле (которую принято называть средней хронологической):

Если промежутки времени между датами неодинаковы, то формула средней хронологической имеет вид:

где t_i - промежуток времени между уровнями .

Средний абсолютный прирост рассчитывается как средняя арифметическая из показателей скорости роста за отдельные промежутки времени:

Средний коэффициент роста показывает, во сколько раз в среднем за отдельные составляющие рассматриваемого периода изменялись уровни динамического ряда. Средний коэффициент роста вычисляется по формуле средней геометрической из коэффициентов роста за отдельные периоды:

Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах:

Средний темп роста, рассчитанный по данным о конечном и начальном уровнях временного ряда, можно использовать только в случае более или менее равномерного изменения уровней.

Средний параболический коэффициент (темп) роста. Если при расчете среднего темпа роста важно обеспечить не только конечный уровень, но и суммарное значение исследуемого показателя за период (например, инвестиции, ввод жилой площади), то средний темп (коэффициент роста) находится из равенства (средней параболической):

(SY_i ) /Y₀ =k + k²+ k³ +….+ kⁿ .

Рассмотрим пример расчета основных показателей ряда динамики.

Пусть имеются данные производстве зерна в одном из хозяйств за пять лет (табл. 2.11, графы 1,2). Рассчитать абсолютные приросты, коэффициенты роста и средние показатели.

Таблица 2.11

Расчет основных показателей динамики

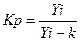
Год	Производство зерна, тыс.ц, yi	Абсолютные приросты DYi-k = Yi – Yi-k	Коэффициент роста	Коэффициент прироста Kпр 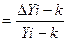, или Kпр = Kпрi-к - 1,0
		-	-	-
			1,08	0,08
			1,148	0,148
			1, 129	0, 129
			1,123	0,123
∑, П			П =1.6	-
Средние	63,2	7,5	1, 125	0, 125

По приведенным формулам рассчитаем абсолютные, относительные и средние показатели. Средний уровень рассчитаем по формуле:

=316/5 = 63,2( табл.11, графа 2).

Ежегодные абсолютные приросты находим как разность между двумя уровнями : DY_i-k = Y_i – Y_i-k ,а средний абсолютный прирост как среднюю арифметическую из показателей скорости роста за отдельные промежутки времени:

( табл., графа 3).

Ежегодные коэффициенты роста (цепные) находим как отношение уровня каждого года к предыдущему:

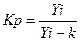, а среднегодовой коэффициент роста рассчитаем как среднюю геометрическую по формуле:

(табл., графа 4).

Если расчет среднего темпа роста ведется с ориентацией на конечный результат, то, как видно из таблицы, средний темп роста равен 112,5%(коэффициент роста равен 1, 125).

Если ориентация берется на достижение суммарного значения (объема) исследуемого показателя за определенный период, то для расчета среднего коэффициента используется средняя параболическая вида

(SY_i ) /Y₀ =k + k²+ k³ +….+ kⁿ , где значение 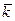определяется по специальной таблице ( см. [1, приложение 10]). Для n =5 и отношения 316/50 = 6,32 находим близкое к нему (6,336), которому соответствует 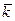= 1, 08. То есть среднегодовой темп роста объемов производства зерна в хозяйстве за пять лет (период с 1999 по 2003 г.) в приведенном примере по средней параболической составлял всего 108,0%, а среднегодовой темп прироста 8,0% ( а не 12, 5 % , как по средней геометрической).