Обозначения на чертежах.

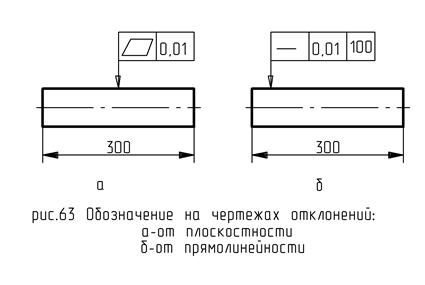
Дан некоторый участок поверхности длинной 300 мм. Мы должны прочитать это следующим образом: отклонение от плоскостности плоскости, к которой направлена стрелка, составляет 0,01 мм на всей поверхности в 300мм.

В случае если нормируется участок поверхности, длина нормирования указывается в обозначениях. Отклонение от прямолинейности на участке (любом) в 100мм не должно превышать допуск на прямолинейность 0,01мм.

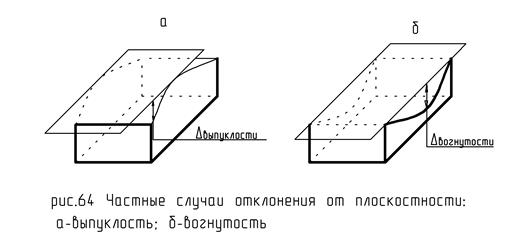
Частными случаями отклонения от плоскостности (прямолинейности) является выпуклость-вогнутость. Если расстояние от реального профиля до прилегающей плоскости (прямой) изменяется монотонно от максимального до нуля и затем опять до максимального, то речь идет о выпуклости, если максимум в центре, то - вогнутость (рис. 64).

Отклонение цилиндрических поверхностей.

Подразделяются на отклонение от цилиндричности, круглости и формы профиля продольного сечения.

Отклонение от цилиндричности.

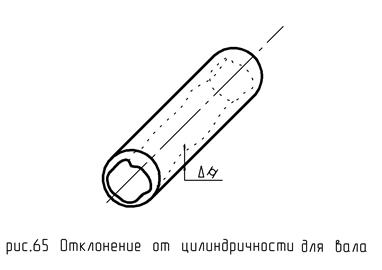
Нормируется относительно прилегающего цилиндра. Для вала - описанного, для отверстия - вписанного.

Верхняя граница поля допуска цилиндричности определяется прилегающим цилиндром (для вала) (для отверстия это будет нижняя граница). Нижняя граница поля допуска соответствует цилиндру, отстоящему от первого на величину допуска. Величина этого допуска приводится в радиальном изображении. Если отклонение меньше допуска, то деталь годная.

Δ_/О/ ≤ Т_/О/.

Отклонение от круглости.

Δ_О ≤ Т_О.

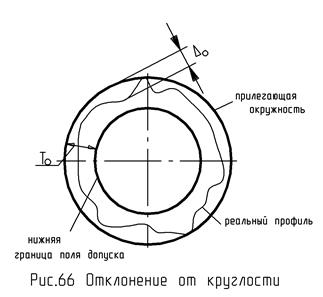
Проводим плоскость нормальную к оси детали. Естественно у нас получился профиль. Описываем вокруг этого реального профиля прилегающую окружность, находим максимальное расстояние от этой прилегающей окружности до какой-то точки профиля. После этого в соответствующих ГОСТах находим величину допуска, откладываем ее. Это нижняя граница поля допуска, она имеет ту же ось, что и прилегающая поверхность.

Частными случаями отклонения от круглости являются овальность и огранка (рис. 67).

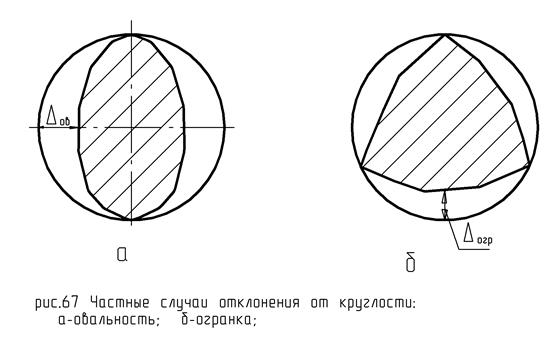
Отклонение формы профиля продольного сечения.

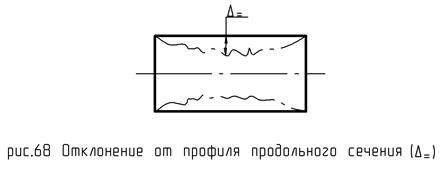
Это наибольшее расстояние от точек профиля (реального) в осевом сечении до соответствующей стороны прилегающего профиля в пределах нормируемого участка L (рис. 68).

Δ₌ ≤ Т₌.

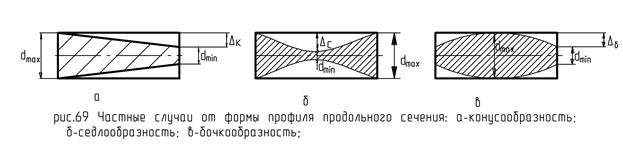
Частными случаями данного отклонения являются конусообразность, седлообразность и бочкообразность (рис. 69).