Основное уравнение молекулярно-кинетической теории идеального газа

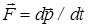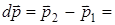
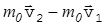Пусть в сосуде в виде куба со стороной l находится N молекул. Рассмотрим движение одной из молекул. Пусть молекула движется из центра куба в одном из 6 возможных направлений (рис.1) , например параллельно оси Х со скоростью v. Ударяясь о стенку А куба молекула оказывает на него давление (см. рис. 2). Найдем его. Согласно второму закону Ньютона сила давления , где . Предполагая, что происходит абсолютно упругий удар, имеем v₁=v₂=v. Изменение импульса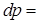 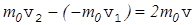. Молекула

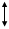
вернется в исходное состояние ( в центр куба) спустя время dt=(0.5l+0.5l)/v=l/v. В итоге получаем выражение для силы давления, оказываемого на стенку сосуда одной молекулой,

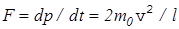. (10)

Если число молекул в сосуде N, то к cтенке А движется

в среднем N/6 молекул и они создают среднюю силу давления на стенку

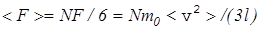, (11)

где <v ²> - cредний квадрат скорости молекул [cм. формулы (17), (18)].

Давление, оказываемое на стенку сосуда, площадь которой S=l²,

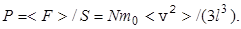(12)

Учитывая, что N/l³=N/V=n, т.е. равно концентрации молекул, а также, что

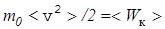(13)

-средняя кинетическая энергия поступательного движения молекулы газа, получаем из (12) основное уравнение молекулярно-кинетической теории идеального газа 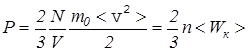. (14) Такое же давление производят молекулы на другие стенки сосуда, поскольку молекулы газа движутся хаотически и не имеют какого-либо преимущественного направления движения.

Итак, согласно (14) давление на стенки сосуда определяется произведением концентрации молекул n на их среднюю кинетическую энергию поступательного движения <W_к>.

1.4. Молекулярно-кинетическое толкование термодинамической температуры Учитывая, что n=N/V=N_A(m/M)/V, где V - объем газа, перепишем (14) в виде 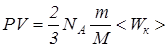. (15)

С другой стороны согласно уравнению Клапейрона-Менделеева РV=(m/M)RT = (m/M)N_AkT. Таким образом

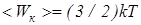. (16)

Итак, термодинамическая температура с точностью до постоянного множителя (3/2)k равна средней кинетической энергии поступательного движения молекулы.

Таково молекулярно-кинетическое толкование термодинамической температуры.

Учитывая, что 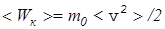, где

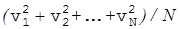<v²>= (17)

средний квадрат скорости молекул газа, из (16) находим среднюю квадратичную скорость <v_KB>= 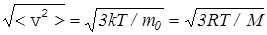. (18)

Например, при t=27° C или T=300 K молекулы кислорода (М=32∙10^-3кг/моль) имеют скорость <v_KB>=483 м/c.