Графоаналитическое определение дисперсии ошибки слежения.

Определение дисперсии и СКО рассмотренным выше методом при больших порядках интеграла (6.14) оказывается затруднительным. Поэтому стали использовать графоаналитический метод [10], в основу которого положен геометрический смысл интеграла: значение интеграла равно площади, которая находится под графиком подынтегральной функции.

Для вычисления дисперсии по формуле (6.13) или (6.11)–(6.13) строят график подынтегральной функции 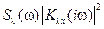+ 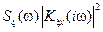(в докомпьютерные времена эти построения выполняли по точкам, взятым на различных частотах ω_j [10]) и вычисляют площадь под ним (в докомпьютерные времена эти вычисления осуществляли с помощью аппроксимации графика и площади под ним прямоугольниками и трапециями [10]).

С учетом четности подынтегральной функции достаточно построить график только для положительных частот (формула (6.9)).

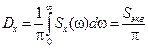. (6.24)

В настоящее время вычисления проще всего проводятся с помощью численного интегрирования в специальных математических программах.

Пример 6.3.Найдем дисперсию для РАС и возмущения, рассмотренных в примере 6.1 (k₀ = 200, S_д = 10).

После подстановки ЧПФ (6.17) и S(ω) формула (6.18) имеет вид

. (6.25)

После подстановки численных значений строим график подынтегральной функции (рис. 6.1) и вычисляем площадь (это удобно сделать с помощью разбиения на 1 прямоугольник и 3 треугольника, как показано на рис. 6.1). После вычисления площадей получаем S_экв ≈ 3,4×10^–3, подставляя в (6.24), вычисляем D_x ≈ 3,4×10^–3/p ≈ 1,08×10^–3.

С помощью численного интегрирования в MathCad можно вычислить площадь и дисперсию (6.20) напрямую: S_экв = 3,32×10^–3, тогда D_x = = 3,32×10^–3/p = 1,06×10^–3, что совпадает с полученным ранее значением.

Пример 6.4.Найдем дисперсию для РАС и возмущения, рассмотренных в примере 6.2. После подстановки численных значений в ЧПФ (формула (6.21)) и S(ω), а затем в формулу (6.18) строим график подынтегральной функции (рис. 6.2) и вычисляем площадь (это удобно сделать с помощью разбиения на 1 трапецию и 1 треугольник).

После вычислений получаем

S_экв ≈ 1,3×10^–3, D_x ≈ 1,3/p ≈ 4,1×10^–4.

При численном интегрировании в MathCad дисперсия D_x = 4,2×10^–4.

Если на РАС действует широкополосная помеха с равномерным спектром, ее можно считать белым шумом. В этом случае вводят понятие эквивалентной шумовой полосы ω_экв(эффективной шумовой полосы ω_эф), под которой понимается величина, равная полосе пропускания эквивалентной РАС с прямоугольной АЧХ, с одинаковой с исходной системой ЧПФ на нулевой частоте (рис. 6.2) и одинаковой дисперсией выходного процесса при действии на входах этих систем белого шума.

Из приведенного определения и выражения (6.13) вытекает (будем рассматривать только положительные частоты f или ω) формула

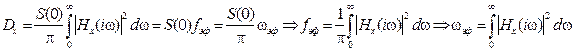. (6.26)

Зная эквивалентную шумовую полосу РАС, сведенную к обобщенному виду, можно легко определить дисперсию по формуле

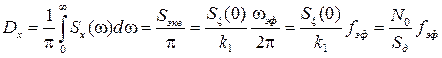. (6.27)

В данном случае в обобщенной РАС действие белого шума приведено ко входу дискриминатора, крутизна которого S_д.

Для графика на рис. 6.1 эквивалентная шумовая полоса ω_эф образует прямоугольник по уровню ≈1×10^–5 и до частоты ω_экв ≈ 330 рад/с.

Для графика на рис. 6.2 эквивалентная шумовая полоса ω_эф образует прямоугольник по уровню ≈9×10^–6 и до частоты ω_экв ≈ 159 рад/с.

Если S(ω) случайного процесса отличается от константы, этот процесс можно свести к белому шуму, добавив в схему устройство, называемое формирующим фильтром [1, 4], на выходе которого процесс будет иметь такую же S(ω).

Важным показателем качества работы нелинейной следящей РАС является вероятность срыва слежения. При выходе ошибки за пределы апертуры дискриминатора (например, под воздействием помех) исчезает напряжение на его выходе, что равносильно по действию размыканию петли регулирования. Через некоторое время ошибка слежения может вновь оказаться в пределах апертуры дискриминатора, и при определенных условиях нормальная работа РАС может возобновиться.

Возникает проблема оценки работоспособности РАС в этих условиях.

Существует понятие «памяти системы». Например, астатическая система первого порядка обладает «памятью по положению». То есть при кратковременном размыкании системы за счет интегратора РАС будет некоторое время удерживать сигнал ошибки в пределах, позволяющих восстановить процесс слежения.

Пример 8.4.Проанализируем условия работы РАС (рис. 8.22) с характеристикой дискриминатора F(x) = c×sin(ax) при воздействии l(t) = l₁t и возмущении x(t) = N₀. Пусть l₁ = 3, N₀ = 10, k_л = 2, T_ф = 1, с = 4, a = 0,1 [2].

Определим математическое ожидание ошибки слежения:

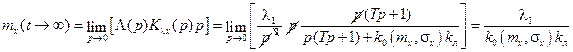. (8.48)

Определим дисперсию ошибки слежения:

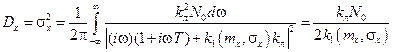. (8.49)

Определим коэффициенты статистической линеаризации и 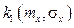по формулам (8.42) – (8.44):

, ,

.

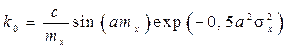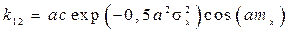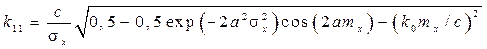Далее необходимо решить уравнения (8.48) и (8.49) совместно относительно переменных m_x и s_x. В [2, 18] это сделано графически, но проще это сделать с помощью «MathCad».

При заданных условиях получаются такие значения: m_x = 4,8; s_x = 5,6; D_x = 31,4.

Для дальнейшего анализа целесообразно построить графики таких зависимосте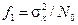й: и 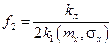(рис. 8.23).

Для исходных данных график 1 соответствует зависимости f₁.

Точка пересечения графиков 1 f₁ и f₂ определяет решение D_x = 31,4.

Срыв слежения в данном случае носит случайных характер. Если увеличить уровень шума (N₀ = 18), то наклон прямой f₁ уменьшится (график 2, f₁₂) до касания с графиком f₂. Это критическое значение при данных условиях.

При большем уровне помех пересечений графиков не будет, решение системы (8.48) и (8.49) не существует – m_x и s_x неограниченно возрастают [2].

График 3 (f₁₃), построенный при N₀ = 30, соответствует именно этому случаю (срыв слежения).

При увеличении математического ожидания график f₂ сместится вверх и критическое значение N₀ уменьшится [2].

При статическом входном воздействии математическое ожидание в установившемся режиме будет равно нулю, а критическое значение N₀ увеличится.