Принцип работы и свойства нелинейной системы ЧАП

Структурная схема ЧАП с преобразованием частоты приведена на рис. 3.3 и описана в линейном режиме в п. 3.2. Построим структурную схему ЧАП (рис. 8.3) с учетом нелинейности характеристики дискриминатора F(Ω) (см. рис. 3.4).

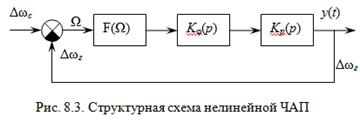
В анализе примем, что нестабильностью частоты ГУН можно пренебречь. Примем, что 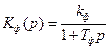; ; 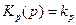W – отклонение частоты на выходе ЧАП (частота ГУН, промежуточная частота) в установившемся режиме от номинального значения (остаточная расстройка).

Составим уравнение работы ЧАП относительно отклонения частоты.

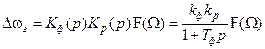. (8.2)

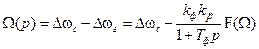. (8.3)

Будем считать, что ЧАП работает в режиме стабилизации частоты (сигналом воздействия является частота эталонного генератора w_эт).

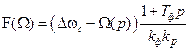. (8.4)

Решим уравнение (8.4) для стационарного режима (t ® ¥ или p ® 0). В этом случае 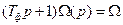и уравнение сводится к виду

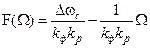. (8.5)

Для наглядности решим уравнение (8.5) графически.

Правая часть (8.5) представляет собой уравнение прямой относительно переменной W.

Решением будут являться точки пересечения (точки 1, 2, 3 на рис. 8.4) этой прямой и графика дискриминационной характеристики F(Ω).

Полученные решения Ω₁, Ω₂, Ω₃ для общего случая (спло­ш­ная прямая a на рис. 8.4) необходимо проанализировать на локальную устойчивость.

Есть несколько способов. Воспользуемся простейшим [2]: линеаризацией характеристики в области каждой точки решения
( ):

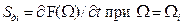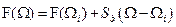. (8.6)

Подстановка (8.6) в (8.4) после замены переменных дает :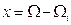

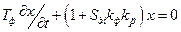. (8.7)

Решение (8.7) и анализ устойчивости [2] приводят к следующим условиям устойчивости решений:

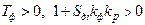. (8.8)

В точке 1 крутизна характеристики S_д1 > 0 и условие устойчивости (8.8) выполняется. В точке 2 S_д2 < 0 и 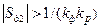– условие (8.8) не выполняется и система неустойчива. В точке 3 S_д3 < 0, но 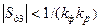, поэтому условие (8.8) выполняется и система устойчива.

Система не может находиться в точке 2, она должна перейти в устойчивое состояние – точку 1 или 3.

В зависимости от начальной расстройки Δω_c (возможные изменения показаны стрелочками на рис. 8.4) уравнение (8.5) может иметь одно или два решения.

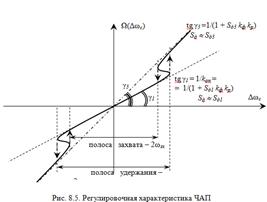
Двум решениям на рис. 8.4 соответствуют штриховые линии b и c. Штриховая линия b позволяет определить по точке пересечения с осью абсцисс полосу захвата (при этом точки 1 и 2 сливаются), а штриховая линия c – полосу удержания (при этом сливаются точки 2 и 3) [24].

Рабочая полоса ЧАП – полоса захвата (точки 1 на рис. 8.4).

Полоса удержания не может быть меньше, чем полоса захвата.

Одному решению, которое получается при нахождении начальной расстройки в полосе захвата, на рис. 8.4 соответствует штрихпунктирная линия d [24].

Зависимость остаточной расстройки Ω от начальной Δω_с называется регулировочной характеристикой и является наиболее информативной характеристикой ЧАП (рис. 8.5) (k_ап = 1 + S_д k_ф k_р).

Система ЧАП является статической РАС с конечной ошибкой 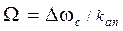(k_ап = 1 + S_д k_ф k_р – коэффициент автоподстройки).

Пусть при включении ЧАП находится в асинхронном режиме, в этом случае начальная расстройка Δω_с находится вне полосы удержания (Δω_с > ω_уд ), частота ГУН равна некоторой собственной частоте (частота при разомкнутой петле ОС). При медленном изменении частоты эталонного генератора в сторону уменьшения рассогласования частот, как только расстройка Δω_с окажется в полосе захвата (Δω_с < ω_зх ), ЧАП войдет в режим слежения (синхронизм, рабочий режим) за частотой сигнала (в режиме стабилизации – за частотой эталонного генератора). При этом частота ГУН меняется скачком и ее отличие от ω_э уменьшается в k_ап раз, в результате частота ГУН почти равна частоте эталонного генератора.

Если теперь начать увеличивать расстройку Δω_с , ЧАП будет работать в синхронном режиме до тех пор, пока значение расстройки будет оставаться внутри полосы удержания (Δω_с < ω_уд ). Чтобы вывести ЧАП из синхронного режима, потребуется увеличить расстройку так, чтобы она оказалась вне полосы удержания (Δω_с > ω_уд ).

Если при включении ЧАП начальная расстройка окажется в полосе захвата (Δω_с < ω_зх ), то система сразу входит в синхронизм.

Если при включении ЧАП начальная расстройка будет лежать в интервале между полосой захвата и удержания ( ω_зх < Δω_с< ω_уд ), то достоверно поведение предсказать нельзя, так как система перейдет в одно из рассмотренных ранее устойчивых состояний.

Максимальная корректирующая расстройка Δω_{k max} , вырабатываемая системой ЧАП, соответствует точке (1 = 2) на рис. 8.4 и равна

Δω_{k max} = k_рS_дU_{д max}, (8.9)

где U_{д max} – максимальное напряжение на выходе дискриминатора.

Соотношение между полосой захвата и удержания оценивается следующими формулами:

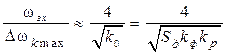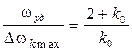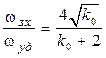; ; . (8.10)

Точность системы прямо пропорциональна k_ап , поэтому для уменьшения установившейся ошибки k_ап следует увеличивать. Однако при этом, как следует из формул (8.10), уменьшается полоса захвата, а значит, уменьшается рабочий диапазон частот эффективной автоподстройки. Таким образом, в статической ЧАП есть противоречие между точностью и полосой эффективной автоподстройки. Для разрешения данного противоречия используют астатическую ЧАП.

В переходном режиме поведение ошибки будет зависеть в основном от характеристики фильтра. Для данного случая 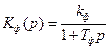, поэтому 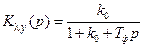, и остаточная расстройка будет изменяться не скачком, а плавно с некоторой задержкой.

На рис. 8.6 приведена ПХ для этого случая.

Время регулирования оценивается формулой .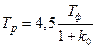

Применение системы ЧАП в РПрмУ по сравнению с ФАПЧ имеет достоинство: ЧАП не реагирует на «зеркальную помеху».