Особенности анализа устойчивости дискретных систем.

После линеаризации нелинейных элементов можно при заданных условиях оценить устойчивость РАС в целом [1, 4].

Для анализа устойчивости нелинейных РАС, выяснения возможности возникновения автоколебаний, определения их частоты и анализа устойчивости автоколебаний применяется метод гармонического баланса.

Суть метода заключается в использовании модификации критерия Найквиста, который применяется к обратной (инверсной) АФЧХ – ОАФЧХ линейной части разомкнутой системы [1, 4].

Вернемся к формуле (8.25), которая связывает компоненты линейной и нелинейной частей разомкнутой РАС: .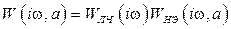

ЧПФ разомкнутой системы зависит не только от частоты входного сигнала, но и от амплитуды.

Критической точкой при использовании критерия устойчивости Найквиста является точка (–1, i0).

Если при изменении ω от 0 до ∞ годограф Найквиста проходит через эту критическую точку, то система будет нейтральна.

В этом случае W(iω, a) = –1, и в РАС могут возникнуть незатухающие колебания (автоколебания). Из формулы (8.25) следует:

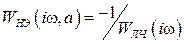или . (8.47)

Анализ на основе выражений (8.47) удобно проводить графически.

Если годографы правой и левой частей не пересекаются, то автоколебания не возникают.

При пересечении годографов (8.47) возможно существование автоколебаний в РАС. Значения частот в точках пересечения годографов определяют частоту автоколебаний. Устойчивость автоколебательного режима оценивается следующим образом [1, 4].

Режим автоколебаний устойчив, если при увеличении амплитуды (по сравнению с исходным значением) годограф нелинейной части перестает охватываться годографом линейной части. То есть для устойчивых автоколебаний в нелинейной РАС необходимо, чтобы с увеличением амплитуды входного сигнала амплитуда автоколебаний уменьшалась.

На рис. 8.19 приведен пример оценки устойчивости нелинейной РАС. График линейной части (сплошная линия на рис. 8.19) пересекает график 2 ОАФЧХ нелинейной части 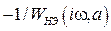в точках a и b, но не имеет точек пересечения с графиком 1. Таким образом, годограф нелинейной части 1 соответствует РАС, в которой автоколебания отсутствуют, а в РАС с годографом 2 могут существовать автоколебания. Точка a соответствует устойчивому режиму, а точка b – неустойчивому (увеличенная амплитуда). Значения амплитуды и частоты в точке a определяют соответственно характеристики автоколебаний.