Типовые примеры и методы их решения
Пример 2.2.1. Найдите величину дисконта, если долговое обязательство на выплату 40 тыс. руб. учтено за 3 года до срока погашения по сложной учетной ставке: а) 20% годовых; б) 25% годовых.
Решение. а) Полагая n = 3, F3=40 тыс. руб., d = 0,2, по формуле (67) получим:
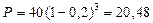 тыс. руб.
тыс. руб.
Поэтому дисконт составит:
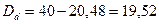 тыс. руб.
тыс. руб.
б) Так как в этом случае d = 0,25, то
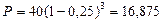 тыс. руб.,
тыс. руб., 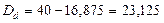 тыс. руб.
тыс. руб.
Видно, что с ростом учетной ставки уменьшается дисконтированная величина выплаты по долговому обязательству и, следовательно, увеличивается величина дисконта.
Пример 2.2.2. Вексель на сумму 70 тыс. руб. со сроком погашения через 4 года учтен за 32 месяца по сложной учетной ставке 24% годовых. Определите суммы, которые получит предъявитель векселя при различных способах учета векселя.
Решение. При применении только сложной учетной ставки воспользуемся формулой (67). Так как дисконтирование производится один раз в год, то n = 32/12 = 8/3. Далее Fn =70 тыс. руб., d = 0,24, поэтому:
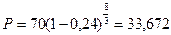 тыс. руб.
тыс. руб.
Если же использовать при учете смешанную схему, то при w = 2, f = 2/3 по формуле (68) получим:
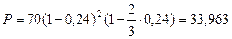 тыс. руб.
тыс. руб.
Таким образом, предъявитель векселя получит больше при использовании смешанной схемы.
Пример 2.2.3. Рассчитайте дисконтированную сумму при учете 1 млн. руб. по простой и сложной учетным ставкам, если годовая учетная ставка равна 18% годовых и учет происходит за 30 дней, 90 дней, 180 дней, 1 год, 2 года, 3 года, 5 лет. Полагать каждый год равным 360 дней.
Решение. Применяя при F = Fn = 1 млн. руб. и d = 0,18 для простой учетной ставки формулу (19), а для сложной - формулу (67), получим следующие результаты, представленные для наглядности в табличном виде:
(млн. руб.)
| Способ дисконтирования | 30 дней (n=1/12) | 90 дней (n=1/4) | 180 дней (n=1/2) | 1 год (n=1) | 2 года (n=2) | 3 года (n=3) | 5 лет (n=5) |
| Простая учетная ставка | 0,985 | 0,955 | 0,91 | 0,82 | 0,64 | 0,46 | 0,1 |
| Сложная учетная ставка | 0,9836 | 0,9516 | 0,9055 | 0,82 | 0,6724 | 0,5514 | 0,3707 |
Таким образом, если вексель на сумму 1 млн. руб. учитывается, когда до срока погашения остается меньше года, то для векселедержателя более выгоден учет по простой учетной ставке. Так, при учете за 90 дней до срока погашения векселедержатель получит: при использовании простой ставки - 955 тыс. руб.; при использовании сложной учетной ставки — 951,6 тыс. руб., т.е. разница между суммами составляет 3,4 тыс. руб. Если же учет векселя осуществляется, когда до срока погашения остается больше года, то для векселедержателя более выгоден учет по сложной учетной ставке.
Заметим, что дисконтирование по простой учетной ставке за срок более чем 5,56 года, приводит к не допустимым на практике величинам (будем получать отрицательные значения дисконтированных сумм). Однако учет по сложной учетной ставке всегда дает положительные дисконтированные величины. Например, при учете за 15 лет получим: 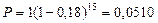 млн. руб.
млн. руб.
Пример 2.2.4. Долговое обязательство на выплату 46 тыс. руб. учтено за 4 года до срока погашения. Определите полученную сумму, если производилось: а) полугодовое; б) поквартальное; в) помесячное дисконтирование по номинальной учетной ставке 24% годовых.
Решение. Во всех случаях полагаем n = 4, Fn = F2 = 46 тыс. руб. и пользуемся формулой (69).
а) Так как m = 2, d(m) =d(2) =0,24, то:
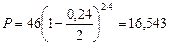 тыс. руб.
тыс. руб.
Поскольку т = 4, d(m) = d(4) = 0,24, то:
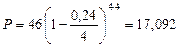 тыс. руб.
тыс. руб.
в) В этом случае т = 12, d(m) = d(12) = 0,24, поэтому:
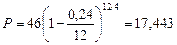 тыс. руб.
тыс. руб.
Сравнивая полученные результаты, видим, что с ростом числа осуществлений операций дисконтирования в году величина учтенного капитала возрастает.
Пример 2.2.5. Определите, какую сумму получит владелец векселя на 30 тыс. руб. со сроком погашения через 25 месяцев, если он учтет вексель сразу при его выдаче по номинальной учетной ставке d(4) =20% годовых. Сравните два способа дисконтирования.
Решение. Полагаем n = 25/12, т = 4, Fп = F25/12 = 30 тыс. руб. Если использовать формулу (69), то
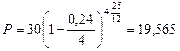 тыс. руб.
тыс. руб.
Пусть дисконтирование осуществляется по смешанной схеме по формуле (70). Поскольку 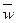 =
= 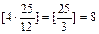 ,
, 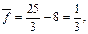 то
то
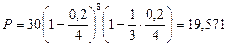 тыс. руб.
тыс. руб.
Очевидно, для векселедержателя выгоднее смешанная схема.
Пример 2.2.6. За долговое обязательство в 80 тыс. руб. банком было выплачено 62 тыс. руб. За какое время до срока погашения было учтено это обязательство, если банком использовалась: а) годовая сложная учетная ставка 28%, б) годовая простая учетная ставка 28%?
Решение. а) Полагая в формуле (71) Р = 62 тыс. руб., Fп = 80 тыс. руб., т = 1, d(4) = 0,28, получим:
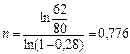 года.
года.
Считая, что в году 360 дней, находим п = 360 • 0,776 = 279,36 дня. Округляя полученный срок до целого числа дней, делаем вывод, что долговое обязательство было учтено за 280 дней до срока погашения.
б) В случае простой учетной ставки воспользуемся формулой (22), где F = 80 тыс. руб., d = 0,28:
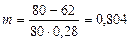 года, или 289,44 дня.
года, или 289,44 дня.
Таким образом, п = 290 дней.
Пример 2.2.7. Вексель был учтен за 2,5 года до срока погашения, при этом владелец векселя получил четверть от написанной на векселе суммы. По какой годовой номинальной учетной ставке был учтен этот вексель, если производилось: а) поквартальное дисконтирование; б) помесячное дисконтирование?
Решение. а) Применяя формулу (72), в которой Р = 0,25Fn, п = 2,5, т = 4, получим:
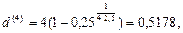 т.е. d(4)=54,78%
т.е. d(4)=54,78%
б) Если т = 12 , то
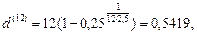 т.е. d(4)=54,19%
т.е. d(4)=54,19%
Таким образом, чем большее количество раз в году производится дисконтирование, тем больше величина годовой номинальной учетной ставки.
Пример 2.2.8. Рассчитайте эффективную годовую учетную ставку при различной частоте начисления дисконта и номинальной учетной ставке, равной 18% годовых.
Решение. Используя формулу (74), вычислим для некоторых значений т эффективную годовую учетную ставку и результаты запишем в табличном виде:
| Т | ||||||
| def | 0,18 | 0,1719 | 0,1682 | 0,1659 | 0,1653 | 0,1648 |
Из таблицы следует, что def уменьшается с ростом т (так как второе слагаемое в правой части равенства (74) увеличивается). Вообще можно показать, что при т > 1 справедливо неравенство def <d(m) которое нетрудно пояснить и из финансовых соображений.
Пример 2.2.9. Определите номинальную учетную ставку, если годовая эффективная учетная ставка равна 30% и дисконтирование по сложной учетной ставке осуществляется: а) каждые полгода; б) ежемесячно; в) ежеквартально.
Решение. Полагаем def =0,3 и пользуемся формулой (73).
a) Так как m = 2, то
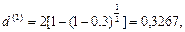 или 32,67%.
или 32,67%.
б)Поскольку в этом случае т =12, то
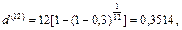 или 35,14%
или 35,14%
в) Считая в году 360 дней, при m=360 получим:
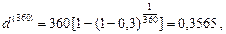 или 35,65%.
или 35,65%.
Найденные номинальные ставки d(2), d(12) и d(360) эквивалентны, так как они получены в соответствии с одной и той же эффективной ставкой. Поэтому осуществление дисконтирования раз в год по сложной учетной ставке 30% годовых дает такой же результат, как осуществление дисконтирования 2 раза в год по ставке 32,67% годовых, или 12 раз в год по ставке 35,14% годовых, или каждый день (360 раз в год) по ставке 35,65% годовых. Отметим, что d(2)<d(12)<d(360), т.е. величина номинальной учетной ставки растет, когда количество осуществлений дисконтирования в году увеличивается. Аналогичное неравенство справедливо и в общем случае, а именно: пусть d(m)и d(1)- эквивалентные номинальные годовые учетные ставки и m > l, тогда d(m)> d(l).
Пример 2.2.10. Вексель на сумму 12 тыс. руб. со сроком погашения через 3 года 6 месяцев был сразу же учтен в банке, и предъявитель векселя получил 5 тыс. руб. Найдите эффективную годовую учетную ставку в этой финансовой операции.
Решение. Подставляя в формулу (75) n = 3,5, Р = 5, F3,5 = 12, находим:
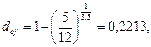 или 22,13%.
или 22,13%.
Пример 2.2.11. По условиям финансового соглашения на сумму 90 тыс. руб., помещенную в банк на 5 лет, начисляются проценты по сложной учетной ставке 24% годовых. Определите наращенную сумму, если начисление процентов производится: а) по полугодиям; б) ежеквартально; в) ежемесячно. Сравните полученные величины с результатами наращения сложными процентами по процентной ставке 24% годовых.
Решение.Будем пользоваться формулой (77), где Р = 90 тыс. руб., п = 5, d(2)= d(12) = d(360) = 0,24. Полагая последовательно m =2, m = 4, m = 12, получим:
а) 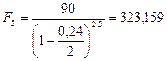 тыс. руб.;
тыс. руб.;
б) 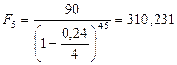 тыс. руб.;
тыс. руб.;
в) 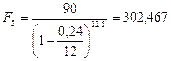 тыс. руб.
тыс. руб.
Полезно заметить, что во всех случаях можно было воспользоваться и формулой (76), полагая число периодов равным соответственно 10, 20 и 60, а учетные ставки – 12% (24% : 2), 6% (24% : 4) и 2% (24% : 12).
Если бы наращение сложными процентами осуществлялось с помощью процентной ставки, то для вариантов а), б), в) получили бы по формуле (58) следующие значения наращенных сумм:
а) 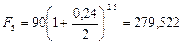 тыс. руб.;
тыс. руб.;
б) 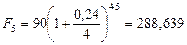 тыс. руб.;
тыс. руб.;
в) 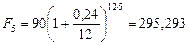 тыс. руб.,
тыс. руб.,
т.е., как уже отмечалось, с увеличением числа начислений процентов за год по сложной процентной ставке величина наращенной суммы возрастает. В противоположность этому с увеличением числа начислений процентов за год по сложной учетной ставке величина наращенной суммы убывает. Видно, что, чем больше число наращений в течение года, тем меньше разница между итоговыми суммами, полученными декурсивным и антисипативным способами начисления процентов. Это и объяснимо, поскольку, чем меньше период начисления, тем меньше отличие между понятиями предварительный и последующий. Так, если m = 365 (каждый день идет начисление сложных процентов), то применение номинальной учетной ставки 24% годовых дает 298,928 тыс. руб., а такой же величины процентной ставки – 298,693 тыс. руб., и разница между этими суммами равна уже 235 руб., в то время как, например, при m = 4 соответствующая разница составляет 21 592 руб.
Пример 2.2.12. Вклад в размере 20 тыс. руб. помещен в банк сроком на 5 лет, причем предусмотрен следующий порядок начисления сложных процентов по плавающей годовой учетной ставке: в первые два года – 16%, в последующие два года – 19% и в оставшийся год – 23%. Найдите наращенную сумму. При использовании какой постоянной сложной учетной ставки можно получить такую же наращенную сумму?
Решение. Наращенную сумму за первые два года определяем по формуле (76), где Fn =20, п = 2, d = 0,16: 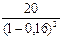 тыс. руб. Наращенную сумму за следующие два года определяем также по формуле (76), где
тыс. руб. Наращенную сумму за следующие два года определяем также по формуле (76), где 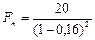 , n = 2, d = 0,19:
, n = 2, d = 0,19: 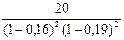 тыс. руб. Аналогичным образом поступая с последним годом, когда d = 0,23; находим, что через 5 лет наращенная сумма составит:
тыс. руб. Аналогичным образом поступая с последним годом, когда d = 0,23; находим, что через 5 лет наращенная сумма составит:
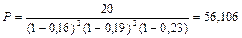 тыс. руб.
тыс. руб.
Годовую (постоянную) учетную ставку 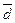 , обеспечивающую такой же результат, как и плавающая ставка, можно найти из равенства
, обеспечивающую такой же результат, как и плавающая ставка, можно найти из равенства 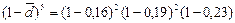 , разрешая его относительно
, разрешая его относительно 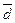 :
:
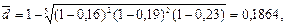 , или 18,64%.
, или 18,64%.
Пример 2.2.13. Банк выдал кредит сроком на 1 месяц под 3% за месяц, удержав проценты при выдаче кредита. Определите доходность такой финансовой сделки для банка в виде годовой эффективной процентной ставки и поясните, как такого рода сделку можно соотнести с начислением сложных процентов по учетной ставке.
Решение. Обозначим через F величину кредита, тогда заемщику выдается сумма F – 0,03F = 0,97F. Теперь можно воспользоваться формулой (64), где Р = 0,97F , Fn=F и n = 1/12 :
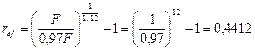 , или 44,12%.
, или 44,12%.
Записывая формулу для вычисления ref; в виде:
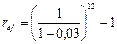
делаем вывод, что начисление процентов один раз за год по процентной ставке 44,12% обеспечивает такой же результат, как и начисление ежемесячно процентов по годовой номинальной учетной ставке d(12) = 3% • 12 = 36% .
Таким образом, выдача банком кредита с одновременным удержанием начисленных процентов по существу означает, что на выданную сумму будут начисляться сложные проценты по учетной ставке.
Пример 2.2.14. Согласно финансовому соглашению банк начисляет по полугодиям проценты на вклады по сложной учетной ставке 28% годовых. Определите в виде простой годовой процентной ставки стоимость привлеченных средств для банка при их размещении: а) на 3 месяца; б) на год.
Решение. а) Стоимость привлеченных средств найдем по формуле (23), где через Р обозначена использованная сумма средств; через F – Р - проценты, выплаченные за использование суммы Р в течение времени n , а F определяется с помощью формулы (77), где п = 0,25 , m = 2 , d(2) = 0,28 . Итак,
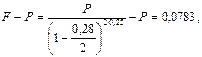
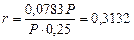 , или 31,32% годовых.
, или 31,32% годовых.
Естественно, можно было и сразу применить формулу (85): 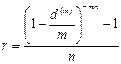 , устанавливающую эквивалентность простой ставки r и сложной учетной ставки d(m):
, устанавливающую эквивалентность простой ставки r и сложной учетной ставки d(m):
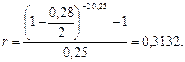
б) Полагая п =1, воспользуемся сразу формулой (85) эквивалентности простой процентной и сложной учетной ставок:
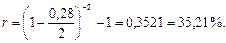
Заметим, что если найти простую учетную ставку, эквивалентную простой процентной ставке r = 35,21%, то она в точности будет равна годовой эффективной учетной ставке, соответствующей номинальной учетной ставке d(2)= 28%. Действительно, по формуле (26):
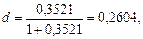
а по формуле (74) получаем то же значение:
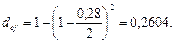
Пример 2.2.15. Вексель учитывается в банке за 3 года до его погашения по сложной учетной ставке 26% годовых. Найдите доходность такой финансовой операции для банка в виде эффективной учетной ставки, если банк удерживает комиссионные в размере 2% от суммы, выплачиваемой за вексель. Как изменится такого рода доходность при учете за 2 года и за 6 лет до срока погашения?
Решение. Пусть за 3 года до срока погашения предъявлен вексель на некоторую сумму F3. Так как сумма, выплачиваемая за вексель, составит: 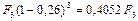 , то величину удерживаемых комиссионных определяем, взяв 2% от этой суммы:
, то величину удерживаемых комиссионных определяем, взяв 2% от этой суммы: 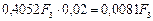 . Следовательно, векселедержатель получит сумму:
. Следовательно, векселедержатель получит сумму: 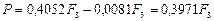 . Теперь по формуле (75) можно определить доходность финансовой операции для банка в виде эффективной учетной ставки:
. Теперь по формуле (75) можно определить доходность финансовой операции для банка в виде эффективной учетной ставки:
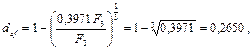
т.е. def = 26,50% , что больше объявленных банком 26% годовых.
Таким образом, удержание комиссионных увеличивает доходность финансовой операции для банка.
При предъявлении векселя за 2 года до срока сумма, выплачиваемая за вексель, составит: 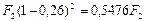 , и поэтому после удержания комиссионных векселедержатель получит сумму:
, и поэтому после удержания комиссионных векселедержатель получит сумму:
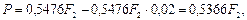

и, следовательно, доходность для банка составит:
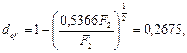
т.е. больше, чем при учете за 3 года.
Аналогичным образом при учете за 6 лет получим:
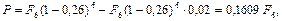
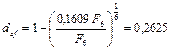
т.е. меньше, чем при учете за 3 года.
Пример 2.2.16.Предприятие приобрело универсальный станок за 320 тыс. руб. Срок службы станка – 8 лет, после чего он реализуется по остаточной стоимости 50 тыс. руб. Используя способ фиксированного процента, составьте таблицу уменьшения стоимости станка по годам.
Решение. В соответствии со способом фиксированного процента стоимость имущества снижается к концу каждого года на одно и то же число процентов d от его стоимости на начало года. Обозначим через Р первоначальную стоимость станка, Pn – остаточную стоимость станка через n лет и получим формулу для определения стоимости станка на конец k-го года.
В конце первого года первоначальная стоимость станка Р будет уменьшена на величину Pd и станет равна P – Pd = P(1 – d). В конце второго года стоимость P(1 – d) будет уменьшена на величину P(1 – d)d и станет равна P(1 – d) – P(1 – d)d = P(1 – d)2. Продолжая аналогичным образом рассуждения, найдем, что в конце k-го года стоимость станка будет равна P(1 – d)k (т.е. сумма P учитывается за k лет по сложной учетной ставке d).
Поскольку в конце n-го года остаточная стоимость станка равна Pn, то получим равенство Pn=P(1 – d)n, из которого можно определить фиксированный процент d снижения стоимости станка: 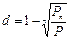 очевидно, эта формула не случайно напоминает формулу (75) определения эффективной годовой учетной ставки). В данном случае срок службы станка составляет n = 8 лет, Р = 320 тыс. руб., Рп = Р8 = =50 тыс. руб., поэтому:
очевидно, эта формула не случайно напоминает формулу (75) определения эффективной годовой учетной ставки). В данном случае срок службы станка составляет n = 8 лет, Р = 320 тыс. руб., Рп = Р8 = =50 тыс. руб., поэтому:
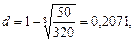 или 20,71%.
или 20,71%.
Далее последовательно находим амортизационные отчисления за год и стоимость станка на конец этого года:
а) в конце первого года:
Pd = 320 • 0,2071 = 66,272 тыс. руб.,
Р -Pd = 320 – 66,272 =253,728 тыс. руб.;
б) в конце второго года:
Р(1 – d)d = 253,728 • 0,2071 = 52,547 тыс. руб.,
P(1 – d)2 = 253,728 - 52,547 = 201,181 тыс. руб.
Продолжая аналогичным образом, получим таблицу:
| Год службы | Амортизационные отчисления за год, тыс. руб. | Стоимость на конец года, тыс. руб. |
| 66,272 | 253,728 | |
| 52.547 | 201,181 | |
| 41,665 | 159,516 | |
| 33,036 | 126,48 | |
| 26.194 | 100,286 | |
| 20,769 | 79,517 | |
| 16,468 | 63,049 | |
| 13,057 | 49,992 |
Наибольшее отличие остаточной стоимости от 50 тыс. руб. (получили 49,992 тыс. руб.) связано с погрешностью приближенных вычислений.
Непрерывная ставка
Основные положения
· При анализе сложных финансовых проблем в банковской практике нередко возникает задача начисления сложных процентов за очень малые промежутки времени. В частности, такая задача особенно актуальна, когда финансовые операции осуществляются и регистрируются с помощью электронных методов. В такого рода ситуациях говорят о непрерывном начислении процентов и их непрерывной капитализации.
· Предел годовой номинальной процентной ставки, когда число начислений сложных процентов стремится к бесконечности, а эффективная ставка постоянна, называется силой роста или интенсивностью наращения за год при непрерывном начислении процентов. Силу роста также еще называют непрерывной ставкой и, чтобы отличать ее от обычной (дискретной), вводят специальное обозначение - 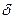 .
.
· При непрерывном начислении процентов исчезает различие между антисипативным и декурсивным способами начисления, так как в такой ситуации начало и конец периода перестают отличаться.
· При использовании непрерывной ставки будущие поступления, являющиеся разновременными суммами, можно оценивать с позиции любого момента времени.
Дата добавления: 2020-10-25; просмотров: 570;











