Типовые примеры и методы их решения

Пример 2.3.1. Рассчитайте накопленную сумму для различных вариантов начисления сложных процентов за один год (равный 360 дням), если исходная сумма Р = 1000 руб. и номинальная годовая процентная ставка r(m) = 30%. Рассмотрите случаи, когда проценты начисляются один раз, по полугодиям, ежеквартально, ежемесячно, ежечасно, ежеминутно, ежесекундно и непрерывно. Для каждого случая определите эффективную годовую процентную ставку.

Решение. Результаты, полученные для всех вариантов, приведем в виде таблицы, причем в четвертом столбце вычислены разности между наращениями с данным числом начисления процентов и базовым, а в пятом столбце указаны разности между наращенными суммами двух соседних строчек.

Р	Частота начисления	F1	Наращение	V
	базовое	цепное
	Ежегодное (т = 1)		-	-	0,3
	Полугодовое (т = 2)	1322,5	22,5	22,5	0,3225
	Ежеквартальное (m = 4)	1335,47	35,47	12,97	0,33547
	Ежемесячное (m = 12)	1344,89	44,89	9,42	0,34489
	Ежедневное (m = 360)	1349,69	49,69	4,8	0,34969
		Ежегодное (m=8640)	1349,85	49,85	0,16	0,34985
		Ежеминутное (m=518400)	1349,86	49,86	0,01	0,34986
		Ежесекундное (m=31104000)	1349,86	49,86		0,34986
		Непрерывное (m= 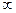)	1349,86	49,86		0,34986

Накопленную сумму и эффективную процентную ставку во всех случаях, кроме последнего, находим соответственно по формулам (58) и (63).

При непрерывном начислении процентов получим:

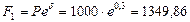руб.,

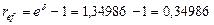
Как и следовало ожидать, приведенные расчеты подтверждают наличие прямой зависимости между частотой начисления процентов и накопленной суммой; пятый столбец таблицы показывает, что с увеличением частоты начисления темп прироста накопленной суммы уменьшается. Если считать с точностью до копеек (что и имеет смысл при практических расчетах и как сделано при заполнении таблицы), то замечаем, что начисление сложных процентов каждую минуту (или за меньший период) доставляет ту же сумму, что и непрерывное начисление процентов. Даже начисление каждый час дает наращенную сумму лишь на 1 копейку меньше.

Эффективная процентная ставка с ростом частоты начисления сложных процентов растет и в пределе достигает величины 34,986%.

Пример 2.3.2. На сумму 6 тыс. руб. в течение 5 лет начисляются непрерывные проценты. Определите наращенную сумму, если сила роста равна: а) 7%; б) 27%.

Решение,а) Полагая Р = 6 тыс. руб., п = 5, 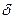= 0,07, по формуле (78) получим:

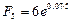тыс. руб.

Если в данном случае применить формулу (55), т.е. осуществлять начисление обычных сложных процентов по процентной ставке r = 0,07, то получим сумму:

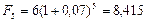тыс. руб.,

которая отличается от предыдущей всего на 99 руб., хотя наращение происходит достаточно долго - 5 лет. Такой результат объясняется небольшой величиной ставки. Ясно, что при более частом начислении сложных процентов эта разница будет еще меньше.

б) Так как в этом случае 5 = 0,27, то

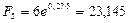тыс. руб.,

Если же воспользоваться формулой (55) при r = 0,27, то получим:

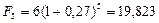тыс. руб.,

т.е. имеем значительную разницу (3,322 тыс. руб.) между найденными суммами.

Пример 2.3.3. Какую сумму необходимо поместить на бан­ковский депозит, чтобы при непрерывном начислении процентов по ставке 25% получить 30 тыс. руб. через: а) 4 года; б) 9 лет?

Решение, а) Для определения искомой суммы воспользуемся формулой (78). Полагая n = 4 , F_n = F₄= 30 тыс. руб., 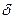= 0,25 , из этой формулы получим:

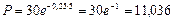тыс. руб.

б) Поскольку n= 9, то

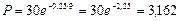тыс.руб.

Пример 2.3.4. За какой срок сумма 10 тыс. руб. достигнет величины 25 тыс. руб. при непрерывном начислении процентов и силе роста 28% за год?

Решение.Полагая в формуле (79) Р_п = 25 тыс. руб., Р = 10 тыс. руб., 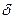= 0,28, находим:

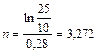года.

Если бы начислялись сложные проценты, например, по годовой номинальной процентной ставке r⁽²⁾ = 0,28, то по формуле (60):

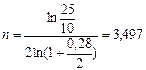года,

т.е., естественно, получили больший срок, чем при непрерывном начислении процентов.

Пример 2.3.5. Банк выдает ссуду на 7 лет под сложную процентную ставку 36% годовых с начислением процентов каждые полгода. Какую непрерывную ставку должен установить банк, чтобы за 7 лет получить тот же доход?

Решение.Пусть Р – величина ссуды, тогда при использовании процентной ставки банк получит через 7 лет (согласно формуле (58)):

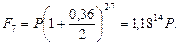
Теперь для определения силы роста можно воспользоваться формулой (80):

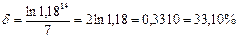
Конечно, этот пример можно было решить, и воспользовавшись сразу формулой (97), связывающей эквивалентные силу роста и сложную процентную ставку.

Пример 2.3.6.Банк предоставил кредит на 4 года под непрерывную ставку 30% за год. Определите доходность такой финансовой операции для банка в виде: а) простой годовой процентной ставки; б) годовой эффективной процентной ставки.

Решение,а) Если Р - величина кредита, то через п - 4 года наращенная сумма, которую заемщик должен будет возвратить, составит:

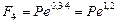
Поэтому доходность в виде простой годовой процентной ставки составит (по формуле (23)):

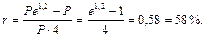
Обратим внимание, что в данном случае по существу была применена формула (93).

б) При определении r_ef воспользуемся формулой (64):

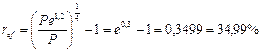
Заметим, что годовая эффективная процентная ставка r_ef и сила роста 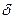связаны соотношением: 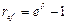, которым мы фактически и воспользовались при решении примера.

Пример 2.3.7. Предприниматель получил в банке ссуду на 6 лет по непрерывной ставке 25% за год, при этом банком были удержаны комиссионные в размере 2% от величины ссуды. Определите доходность такой финансовой операции для банка в виде: а) простой годовой процентной ставки; б) годовой эффективной процентной ставки, если непрерывные проценты начисляются на исходную величину ссуды.

Решение.а) Обозначим через Р величину ссуды, тогда величина удержанных комиссионных составит 0,02P и господину N будет выдана сумма Р - 0,02Р = 0,98Р . Через 6 лет господин N должен будет вернуть (согласно формуле (78)) сумму, равную 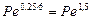. Банк вычисляет доходность сделки исходя из условия: наращенная по простой процентной ставке r на реально выданную ссуду сумма 0,98P(1 + 6r) должна быть равна возвращаемой господином N через 6 лет сумме Ре^1,5. Таким образом, доходность сделки r определяется из уравнения: 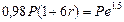. Откуда:

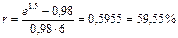
По существу воспользовались формулой (23).

б) В этом случае наращенная по эффективной процентной ставке r_ef на реально выданную ссуду сумма составит 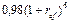и, следовательно, получим уравнение: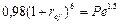

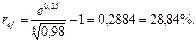
Пример 2.3.8. На вклад 16 тыс. руб. начисляются непрерывные проценты. Определите наращенную сумму за 6 лет, если интенсивность наращения изменяется следующим образом: в первые два года она равна 20%, в следующие три года – 24% и в последний год – 26%. Какую постоянную силу роста необходимо взять, чтобы за 6 лет получить такую же наращенную сумму?

Решение.Пусть Р = 16 тыс. руб. По формуле (78) за первые два года при силе роста 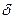= 0,2 наращенная сумма составит:

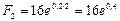тыс. руб.,

Далее наращение суммы F₂ непрерывными процентами за три года при 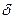= 0,24 обеспечит величину:

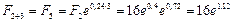тыс. руб.

И наконец, за последний год получим при 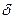= 0,26:

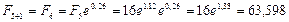тыс. руб.

Такую же наращенную сумму за 6 лет можно получить, если в качестве постоянной силы роста взять

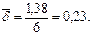
Заметим, что 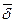представляет собой взвешенную сумму исходных непрерывных ставок, где весом для каждой ставки является доля времени (от общего срока 6 лет), в течение которого использовалась данная ставка. Действительно:

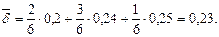
Пример 2.3.9.Господин N намеревается обменять имеющиеся у него немецкие марки и поместить полученную сумму на рублевом депозите сроком на 2 года под ставку 21% годовых с непрерывным начислением процентов, после чего наращенную сумму опять конвертировать в немецкие марки. При каком ожидаемом курсе продажи не имеет смысла такая финансовая операция, если курс покупки немецких марок на начало срока составляет 10 руб. 64 коп, и на валютном депозите денежную сумму можно поместить под процентную ставку 18% годовых с ежеквартальным начислением сложных процентов?

Решение. Обозначим через Р имеющуюся первоначальную сумму немецких марок, через К - ожидаемый курс продажи немецких марок через 2 года, при котором нет смысла в двойном конвертировании. Неизвестную величину К находим, приравнивая наращенные суммы на валютном и на рублевом депозитах с учетом конвертации:

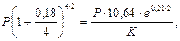
отсюда 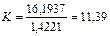руб. Если ожидаемый курс продажи будет менее 11 руб. 39 коп., то финансовая операция, связанная с двойной конвертацией, целесообразна.

Пример 2.3.10.Сумма 15 тыс. руб. была помещена в банк на некоторый срок, по истечении которого на эту сумму были начислены непрерывные проценты с силой роста 30% за год. После уплаты налога на проценты величина наращенной суммы составила 36,2 тыс. руб. Определите срок, за который было осуществлено наращение, если ставка налога на проценты равна 12% и налог на все полученные проценты был выплачен один раз в конце срока.

Решение.Воспользуемся соотношением (101), разрешая его относительно п:

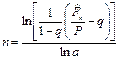
Так как в этом случае Р = 15 тыс. руб., 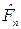=36,2 тыс. руб., q=0,12, a=e^0,3 и lna=0,3, то

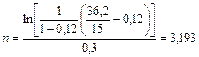года.

С целью проверки применим непосредственно формулу (101):

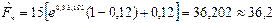тыс. руб.

Пример 2.3.11.Сумма 15 тыс. руб. была помещена в банк на некоторый срок, в течение которого на сумму начислялись непрерывные проценты с силой роста 30% за год. После уплаты налога на все начисленные проценты величина итоговой наращенной суммы составила 36,2 тыс. руб. Определите срок, в течение которого осуществлялось наращение, если ставка налога на проценты равна 12% и налог на проценты уплачивается каждый год путем выделения средств из накапливаемой суммы.

Решение.Выражая из равенства (102) п, в обозначениях предыдущего примера находим:

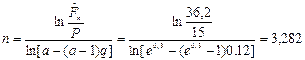года,

т.е. получен больший по величине срок, чем в предыдущем случае.