Виды дифференциации продукта. Горизонтальная (пространственная) продуктовая дифференциация. Модель линейного города (модель Хотеллинга). Модель кругового города (модель Салопа)
Горизонтальную дифференциацию рассмотрим на модели Хотеллинга. Дифференциация осуществляется по местоположению. Рассматривается город, в котором только 2 магазина торгуют хлебом. В этом случае не существует по характеристикам ни плохих, ни хороших продуктов, т. е. продукты (хлеб) одинаковы. Магазины расположены на противоположных концах города. Расстояние между ними = 1. Магазин 1 расположен в точке Х = 0, а магазин 2 – в точке Х = 1. На всем расстоянии между магазинами продавцы расположены равномерно. В течение дня каждый покупатель покупает только либо 1 буханку хлеба, либо нуль. Предпочтения покупателей одинаковы, каждых готов заплатить за товар максимум λ. Транспортные расходы на единицу товара составляют t на единицу расстояния. Для каждого продавца чистая цена, которую он может получить от продажи единицы товара зависит от:
1) от максимальной готовности платить за товар λ.
2) от расстояния между продавцом и покупателем
Для первого продавца она равна:
Р1 = λ – t Х,
где Х – расположение покупателя, оно определяется интервалом [0,1].
Для второго продавца (рис. 9.1) – равна
Р2 = λ – t( 1–Х).
| Х' |
| Зона ценовой конкуренции 1-й и 2-й фирм |
| Зона монопольной власти 1-й фирмы |
| Зона монопольной власти 2-й фирмы фирмы |
| Р2(Х1) |
| Р2 |
| Р1(Х1) |
| Р1 |
| Х1 |
Рис. 9.1. Модель Хотеллинга горизонтальной дифференциации продукта
Определим спрос на товар первого продавца. В зоне монопольной власти он определятся ценой товара Р1 и находим его из формулы:
Р1 = λ – t Х Отсюда: D(Х1) = (λ – Р1) / t
Второй участок спроса продавца 1 соответствует области ценовой конкуренции. Поэтому спрос на его продукт будет только в том случае, если он установит такую же цену, как и продавец 2:
Р1 = λ – t Х1= Р2 = λ – t( 1– Х1)
Следовательно, можно записать:
Р2 – Р1 = (λ – t( 1–Х1)) – (λ – t Х1) = λ – t+ t Х1 –λ + t Х1 = – t + 2t Х1, т.е.
2t Х1 = (Р2 – Р1) + t D(Х1) = 0,5 + (Р2 – Р1) / 2 t
Подчеркнутые формулы определяют спрос на продукт первого продавца.
Данную модель можно рассматривать как общую модель дифференциации продукта, если считать, что; а) расстояние между продавцами отражает различие потребительских характеристик двух производителей; б) транспортные расходы рассматривать как денежный эквивалент потери полезности потребителя, предпочитающего крепкое пиво, но вынужденного пить безалкогольное.
Таким образом, аппарат модели Хотеллинга позволяет сделать вывод: рост приверженности марке снижает ценовую конкуренцию и укрепляет основы монопольной власти.
Модель Хотеллинга с фиксированными ценами
Рассмотрим поведение фирм в отношении дифференциации продукта, если цены на продукт будут фиксированы (например, их устанавливает государство). Предположим, что Магазин А расположен на одном конце улицы, а магазин Б на другом, на расстоянии 1. Причем магазин Б не может быстро изменить свое положение. Тогда магазин А будет стремиться занять такое положение, при котором его прибыль возрастет (рис. 9.2).
Рис.9.2. Окончательный выбор местоположения фирмы при фиксированной цене
При отсутствии свободы ценообразования продавцы выбирают минимальный уровень дифференциации продукта, что ведет к отклонению от оптимального для общества числа торговых марок.
Модель «кругового города» (модель Салопа)
В модели Салопа рассматривается долгосрочная динамика на рынке дифференцированного продукта: решения фирм о входе на рынок и выходе с рынка под воздействием изменения экономической прибыли результате ценовой конкуренции.
Предположим, город, опоясывает улица, протяженность которой =1. Ставка транспортного тарифа t измеряет приверженность торговой марке. Всего n фирм и они расположены вдоль окружности (улицы) а одинаковом расстоянии друг от друга. Предельные издержки фирм одинаковы и равны МС. Необратимые (невозвратные) издержки входа для фирмы составляют f. Если в долгосрочном периоде новая фирма входит на рынок, то все остальные продавцы перестраиваются, занимая положение на расстоянии 1/ n друг от друга (рис.9.3). Покупатели равномерно распределены вдоль окружности и имеют одинаковые предпочтения. Их максимальная готовность платить за товар равна λ.
Рис 9.3. Расположение фирм-продавцов на рынке в модели Салопа
Допустим, при данном значении t для потребителей характерна максимальная готовность платить.
Случай 1. Фирм на рынке мало. Они расположены далеко друг от друга и поэтому каждая из них обладает монопольной властью. Ценовая конкуренция между ними невозможна (рис.9.4).
| i + 1 |
| i |
| i – 1 |
| Pi + 1 |
| Pi |
| Pi – 1 |
Рис 9.4. Модель Салопа: случай 1
Случай 2. Фирм на рынке много, продавцы расположены достаточно близко друг к другу и ценовая конкуренция между ними возможна (рис.9.5).
| Х′ |
| i + 1 |
| i |
| i – 1 |
| Pi + 1 |
| Pi |
| Pi – 1 |
Рис 9.5. Модель Салопа: случай 2
При данном числе продавцов в краткосрочном периоде в результате конкуренции установится равновесная цена, равная:
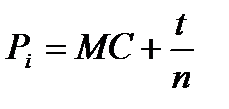
Прибыль каждого продавца составляет 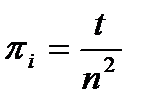
В долгосрочном периоде сумма прибыли будет равна:
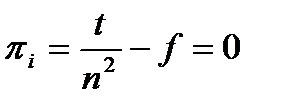
Число продавцов на рынке составит 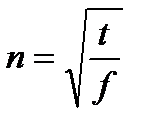 .
.
Дата добавления: 2016-07-27; просмотров: 3586;











