ОСНОВНЫЕ СВЕДЕНИЯ О МЕТОДАХ АНАЛИЗА ЛИНЕЙНЫХ РАС
Кдинамическим характеристикам относят частотныеивременные характеристики.
Частотные характеристики показывают изменения модуля и аргумента комплексного коэффициента передачи в функции от частоты гармонического входного воздействия. Аргумент временных характеристик – время.
Свойства линейного динамического звена (как и всей системы) могут быть количественно и качественно описаны через его ПФ.
Передаточная функция (ПФ).Различают ПФ в операторной форме, в форме изображений Лапласа и частотные ПФ.
Из-за наличия инерционных элементов и преобразований энергии процессы в РАС обычно описываются дифференциальными уравнениями.
Часто используется операторная форма (p= d/dt, y(n)→pn).
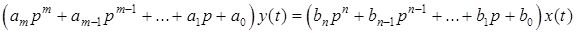 . (1.1)
. (1.1)
ПФ Kyx(p) в операторной форме отражает способность звена преобразовывать входное воздействие
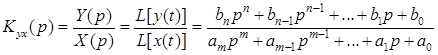 . (1.2)
. (1.2)
где L – оператор прямого преобразования Лапласа (прил. 1).
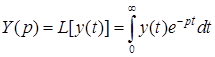 , (1.3)
, (1.3)
есть прямое преобразование Лапласа выходного процесса.
От ПФ в операторной форме в стационарном режиме можно перейти к частотной ПФ (ЧПФ), заменив оператор p на переменную iw, где 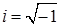 – мнимая единица.
– мнимая единица.
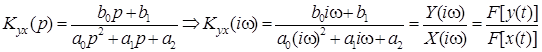 . (1.4)
. (1.4)
Y(iw) – спектральная характеристика выходного процесса, полученная как прямое преобразование Фурье F[y(t)] от временной функции y(t)
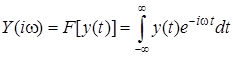 . (1.5)
. (1.5)
ЧПФ есть комплексный коэффициент передачи системы по частоте w.
Частотные свойства ЧПФ отображают также в виде графика – годографа. Годограф ЧПФ строят либо в полярной, либо в декартовой системе координат. При этом соответственно пользуются экспоненциальной или алгебраической формами записи комплексного числа
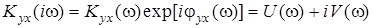 . (1.6)
. (1.6)
Соответствующий график содержит информацию о модуле – Kyx(ω), фазе – φyx(ω) и циклической частоте ω. Так как каждая его точка соответствует определенной фиксированной частоте, его называют амплитудно-фазово-частотной характеристикой (АФЧХ).
Амплитудно-частотная характеристика (АЧХ) строится по формуле
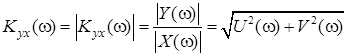 , (1.7)
, (1.7)
где Y(ω) и X(ω) – комплексные амплитуды процессов на частоте ω.
Фазово-частотная характеристика (ФЧХ) представляется в виде
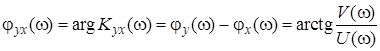 . (1.8)
. (1.8)
Графики АЧХ и ФЧХ имеют линейный масштаб по оси абсцисс.
Временные характеристики.T – постоянная времени цепи, которая характеризует быстродействие звена, ее можно определить графически, если провести касательную к кривой h(t) (ПХ) в точке h(0) (рис. 1.1).
 Для звеньев первого порядка время регулирования может быть определено как Tpег= (4...5)T [1].
Для звеньев первого порядка время регулирования может быть определено как Tpег= (4...5)T [1].
При исследовании ПХ динамических звеньев в виде электрических цепей создать единичный скачок напряжения несложно. Для этого, в частности, можно использовать периодическую последовательность прямоугольных импульсов, длительность которых будет существенно больше Tpег звена.
Амплитуда импульсов должна выбираться с таким расчетом, чтобы не нарушились условия линейности звена.
Импульсная характеристика (ИХ) – g(t) определяет поведение процесса на выходе системы при воздействии на ее входе дельта-импульса (d(t) – функции Дирака) при нулевых начальных условиях.
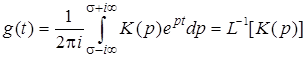 – (1.9)
– (1.9)
обратное преобразование Лапласа ПФ K(p); а
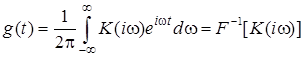 – (1.10)
– (1.10)
обратное преобразование Фурье ЧПФ K(iw).
ИХ, как и ПХ h(t), АФЧХ, совокупность ЛАЧХ и ЛФЧХ, также позволяет определить все параметры линейного звена.
В условиях эксперимента можно сформировать воздействие d(t) лишь приближенно, например использовать короткий импульс, длительность которого много меньше постоянной времени звена (Ти << Т). Рекомендуется выбирать Ти из отношения Ти < Т/(20…50).
Дата добавления: 2020-10-25; просмотров: 567;











